题目内容
5．化简：$\frac{{a}^{2}-4}{{a}^{2}+2a+1}$÷$\frac{{a}^{2}-4a+4}{（a+1）^{2}}$-$\frac{2}{a-2}$的结果为（ ）| A． | $\frac{a+2}{a-2}$ | B． | $\frac{a-4}{a-2}$ | C． | $\frac{a}{a-2}$ | D． | a |
分析 先将分式的分子分母因式分解，同时将除法转化为乘法，再计算分式的乘法，最后计算分式的加法即可．
解答 解：原式=$\frac{（a+2）（a-2）}{（a+1）^{2}}$×$\frac{（a+1）^{2}}{（a-2）^{2}}$-$\frac{2}{a-2}$
=$\frac{a+2}{a-2}$-$\frac{2}{a-2}$
=$\frac{a}{a-2}$，
故选：C．
点评 本题主要考查分式的混合运算，熟练掌握分式的混合运算顺序和运算法则是解题的关键．
练习册系列答案
相关题目
15．下列分式运算，正确的是（ ）
| A． | （$\frac{2y}{3x}$）2=$\frac{2{y}^{2}}{3{x}^{2}}$ | B． | $\frac{1}{x-y}-\frac{1}{y-x}=0$ | C． | $\frac{1}{3x}+\frac{1}{3y}=\frac{1}{3（x+y）}$ | D． | （$\frac{{x}^{2}}{-y}$）3=$-\frac{{x}^{6}}{{y}^{3}}$ |
13．
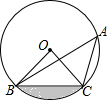如图，点A、B、C在⊙O上，若∠BAC=45°，OB=2，则图中阴影部分的面积为（ ）
如图，点A、B、C在⊙O上，若∠BAC=45°，OB=2，则图中阴影部分的面积为（ ）| A． | π-4 | B． | $\frac{2}{3}π-1$ | C． | π-2 | D． | $\frac{2π}{3}-2$ |
20．
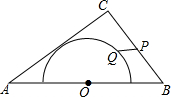如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（ ）
如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（ ）| A． | 6 | B． | 2$\sqrt{13}$+1 | C． | 9 | D． | $\frac{32}{2}$ |
10．某机加工车间共有26名工人，现要加工2100个A零件，1200个B零件，已知每人每天加工A零件30个或B零件20个，问怎样分工才能确保同时完成两种零件的加工任务（每人只能加工一种零件）？设安排x人加工A零件，由题意列方程得（ ）
| A． | $\frac{2100}{30x}$=$\frac{1200}{20（26-x）}$ | B． | $\frac{2100}{x}$=$\frac{1200}{26-x}$ | ||
| C． | $\frac{2100}{20x}$=$\frac{1200}{30（26-x）}$ | D． | $\frac{2100}{x}$×30=$\frac{1200}{26-x}$×20 |
17．A，B两地相距180km，新修的高速公路开通后，在A，B两地间行驶的长途客车平均车速提高了50%，而从A地到B地的时间缩短了1h．若设原来的平均车速为xkm/h，则根据题意可列方程为（ ）
| A． | $\frac{180}{x}$-$\frac{180}{（1+50%）x}$=1 | B． | $\frac{180}{（1+50%）x}$-$\frac{180}{x}$=1 | ||
| C． | $\frac{180}{x}$-$\frac{180}{（1-50%）x}$=1 | D． | $\frac{180}{（1-50%）x}$-$\frac{180}{x}$=1 |
14．计算a10÷a2（a≠0）的结果是（ ）
| A． | a5 | B． | a-5 | C． | a8 | D． | a-8 |
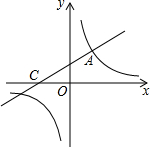如图，直线y=$\frac{1}{2}$x+2与双曲线相交于点A（m，3），与x轴交于点C．