题目内容
9.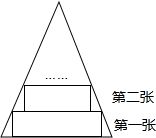 如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )| A. | 第4张 | B. | 第5张 | C. | 第6张 | D. | 第7张 |
分析 根据相似三角形的相似比求得顶点到这个正方形的长,再根据矩形的宽求得是第几张.
解答 解:已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是3,
所以根据相似三角形的性质可设从顶点到这个正方形的线段为x,
则$\frac{3}{18}=\frac{x}{18}$,解得x=3,
所以另一段长为18-3=15,
因为15÷3=5,所以是第5张.
故选:B.
点评 本题主要考查了相似三角形的性质及等腰三角形的性质的综合运用;由相似三角形的性质得出比例式是解决问题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
19.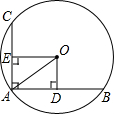 如图,在⊙O中,弦AB⊥AC,OD⊥AB于点D,OE⊥AC于点E,若AB=8cm,AC=6cm,则⊙O的半径OA的长为( )
如图,在⊙O中,弦AB⊥AC,OD⊥AB于点D,OE⊥AC于点E,若AB=8cm,AC=6cm,则⊙O的半径OA的长为( )
 如图,在⊙O中,弦AB⊥AC,OD⊥AB于点D,OE⊥AC于点E,若AB=8cm,AC=6cm,则⊙O的半径OA的长为( )
如图,在⊙O中,弦AB⊥AC,OD⊥AB于点D,OE⊥AC于点E,若AB=8cm,AC=6cm,则⊙O的半径OA的长为( )| A. | 7cm | B. | 6cm | C. | 5cm | D. | 4cm |
20.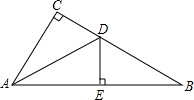 如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )
如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )
 如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )
如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )| A. | AB=2AE | B. | AC=2CD | C. | DB=2CD | D. | AD=2DE |
17.抛物线y=-4x2+5的开口方向( )
| A. | 向上 | B. | 向下 | C. | 向左 | D. | 向右 |
1.在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
| A. | $sinA=\frac{{\sqrt{3}}}{2}$ | B. | $cosA=\frac{{\sqrt{3}}}{2}$ | C. | $tanA=\frac{1}{2}$ | D. | $cotA=\frac{{\sqrt{3}}}{3}$ |
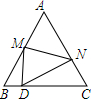 如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么$\frac{AM}{AN}$的值为$\frac{5}{7}$.
如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么$\frac{AM}{AN}$的值为$\frac{5}{7}$.
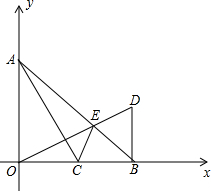 如图,在平面直角坐标系中,点A(0.4),B(4,0),C为OB的中点,连AC,OE⊥AC交AB于E,BD⊥x轴交OE的延长线于D.
如图,在平面直角坐标系中,点A(0.4),B(4,0),C为OB的中点,连AC,OE⊥AC交AB于E,BD⊥x轴交OE的延长线于D.