题目内容
14.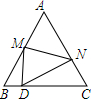 如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么$\frac{AM}{AN}$的值为$\frac{5}{7}$.
如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么$\frac{AM}{AN}$的值为$\frac{5}{7}$.
分析 由BD:DC=1:3,可设BD=a,则CD=3a,根据等边三角形的性质和折叠的性质可得:BM+MD+BD=5a,DN+NC+DC=7a,再通过证明△BMD∽△CDN即可证明AM:AN的值.
解答 解:∵BD:DC=1:3,
∴设BD=a,则CD=3a,
∵△ABC是等边三角形,
∴AB=BC=AC=4a,∠ABC=∠ACB=∠BAC=60°,
由折叠的性质可知:MN是线段AD的垂直平分线,
∴AM=DM,AN=DN,
∴BM+MD+BD=5a,DN+NC+DC=7a,
∵∠MDN=∠BAC=∠ABC=60°,
∴∠NDC+∠MDB=∠BMD+∠MBD=120°,
∴∠NDC=∠BMD,
∵∠ABC=∠ACB=60°,
∴△BMD∽△CDN,
∴(BM+MD+BD):(DN+NC+CD)=AM:AN,
即AM:AN=5:7,
故答案为$\frac{5}{7}$.
点评 本题考查了等边三角形的性质、全等三角形的判定和性质以及折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
5.用长为16m的木条围成一个矩形框架,设矩形面积为S(m2),则S的最大值为( )
| A. | 8m2 | B. | 16m2 | C. | 12m2 | D. | 32m2 |
9.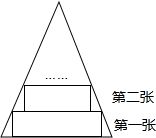 如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
 如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )| A. | 第4张 | B. | 第5张 | C. | 第6张 | D. | 第7张 |
19.如果两个相似三角形的面积比是1:4,那么它们的周长比是( )
| A. | 1:16 | B. | 1:4 | C. | 1:6 | D. | 1:2 |
7.把分式$\frac{2a}{a+b}$中的a、b都扩大5倍,则分式的值( )
| A. | 扩大10倍 | B. | 不变 | C. | 扩大5倍 | D. | 缩小5倍 |