题目内容
19．
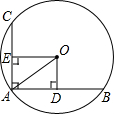如图，在⊙O中，弦AB⊥AC，OD⊥AB于点D，OE⊥AC于点E，若AB=8cm，AC=6cm，则⊙O的半径OA的长为（ ）| A． | 7cm | B． | 6cm | C． | 5cm | D． | 4cm |
分析 根据垂径定理求得OD，AD的长，并且在直角△AOD中运用勾股定理即可求解．
解答 解：∵弦AB⊥AC，OD⊥AB于点D，OE⊥AC于点E，
∴四边形OEAD是矩形，AD=$\frac{1}{2}$AB=4cm，AE=$\frac{1}{2}$AC=3cm，
∴OD=AE=3cm，
∴OA=$\sqrt{O{D}^{2}+A{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5（cm）；
故选：C．
点评 本题考查了垂径定理、勾股定理、矩形的判定与性质；利用垂径定理求出AD，AE的长是解决问题的关键．
练习册系列答案
相关题目
9．在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以点C为圆心2cm长为半径的圆与AB的位置关系是（ ）
| A． | 相交 | B． | 相切 | C． | 相离 | D． | 不能确定 |
10．
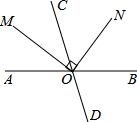如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠AOM=30°，则∠CON的度数为（ ）
如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠AOM=30°，则∠CON的度数为（ ）| A． | 30° | B． | 40° | C． | 60° | D． | 50° |
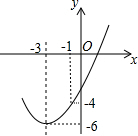如图，已知顶点为（-3，-6）的抛物线y=ax2+bx+c经过点（-1，-4），下列结论：①b2＞4ac；②ax2+bx+c≥-6；③若点（-2，m），（-5，n）在抛物线上，则m＞n；④关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1，其中正确的有（ ）
在美化校园的活动中，某兴趣小组想借助如图6所示的直角墙角（CD边所在的墙长10米，DA边所在的墙足够长），用28米长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=x米．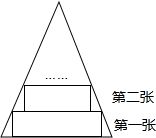
如图所示，一张等腰三角形纸片，底边长18cm，底边上的高长18cm，现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条，已知剪得的纸条中有一张是正方形，则这张正方形纸条是（ ）