题目内容
4．在坐标平面内，△ABC三个顶点的坐标分别是A（3，5）、B（-4，3）、C（5，-5），求△ABC的面积．分析 在平面直角坐标系中画出三角形ABC，通过割补法将三角形补充成一个正方形，然后用正方形面积减去三个三角形面积即为所求．
解答 解：将A（3，5）、B（-4，3）、C（5，-5）在平面直角坐标系描出，
画出△ABC如下：
过A、B、C三点分别作x轴y轴垂线，交点分别为E、D、F、C，
则E（-4，5）、D（5，5）、F（-4，-5）、C（5，-5），
S△ABC=S四边形CDEF-S△AEB-S△BFC-S△CDA
=9×10-$\frac{1}{2}$×7×2-$\frac{1}{2}$×8×9-$\frac{1}{2}$×10×2
=90-7-36-10
=37．
∴△ABC的面积为37．
点评 题目考查了坐标图形的面积，解决题目的关键是通过割补法找到三角形面积的等量关系．题目难易程度适中，适合学生课后训练．
练习册系列答案
相关题目
14．
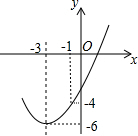如图，已知顶点为（-3，-6）的抛物线y=ax2+bx+c经过点（-1，-4），下列结论：①b2＞4ac；②ax2+bx+c≥-6；③若点（-2，m），（-5，n）在抛物线上，则m＞n；④关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1，其中正确的有（ ）
如图，已知顶点为（-3，-6）的抛物线y=ax2+bx+c经过点（-1，-4），下列结论：①b2＞4ac；②ax2+bx+c≥-6；③若点（-2，m），（-5，n）在抛物线上，则m＞n；④关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1，其中正确的有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
15．
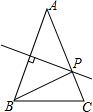如图．△ABC中，AB=AC，AB的垂直平分线交AC于P点，若AB=6cm，BC=4cm，△PBC的周长等于（ ）
如图．△ABC中，AB=AC，AB的垂直平分线交AC于P点，若AB=6cm，BC=4cm，△PBC的周长等于（ ）| A． | 4cm | B． | 6cm | C． | 8cm | D． | 10cm |
12．下列计算正确的是（ ）
| A． | a3÷a2=a | B． | （-2a2）3=8a6 | C． | 2a2+a2=3a4 | D． | （a-b）2=a2-b2 |
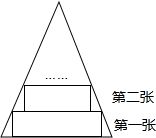如图所示，一张等腰三角形纸片，底边长18cm，底边上的高长18cm，现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条，已知剪得的纸条中有一张是正方形，则这张正方形纸条是（ ）
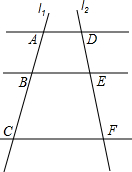如图，已知AD∥BE∥CF，它们依次交直线l1、l2于点A、B、C和点D、E、F，$\frac{DE}{EF}=\frac{2}{5}$，AC=14；