题目内容
2.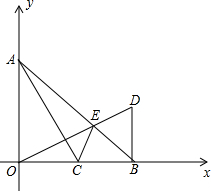 如图,在平面直角坐标系中,点A(0.4),B(4,0),C为OB的中点,连AC,OE⊥AC交AB于E,BD⊥x轴交OE的延长线于D.
如图,在平面直角坐标系中,点A(0.4),B(4,0),C为OB的中点,连AC,OE⊥AC交AB于E,BD⊥x轴交OE的延长线于D.(1)求证:△AOC≌△OBD;
(2)求点D的坐标;
(3)已知∠OAB=∠OBA,线段AC、CE、0E是否存在某种确定的数量关系?写出你的结论,并加以证明.
分析 (1)如图,由A点和B点坐标得OA=OB=4,再利用等角的余角相等得∠1=∠2,于是可根据“ASA”判断△AOC≌△OBD;
(2)由C为OB的中点得到OC=BC=2,再由△AOC≌△OBD得到OC=BD=2,则可写出D点坐标;
(3)先证明∠OAB=∠OBA=∠DBE=45°,则可根据“SAS”证明△BCE≌△BDE,所以CE=DE,再由△AOC≌△OBD得到AC=OD,所以OD=OE+DE=OE+CE=AC.
解答 (1)证明:如图,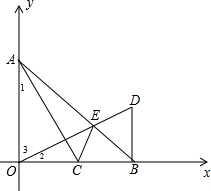
∵A(0.4),B(4,0),
∴OA=OB=4,
∵OE⊥AC,
∴∠3+∠1=90°,
而∠3+∠2=90°,
∴∠1=∠2,
∵BD⊥x轴,
∴∠DBO=90°,
在△AOC和△OBD中
$\left\{\begin{array}{l}{∠1=∠2}\\{AO=OB}\\{∠AOC=∠OBD}\end{array}\right.$,
∴△AOC≌△OBD;
(2)解:∵C为OB的中点,
∴OC=BC=2,
∵△AOC≌△OBD,
∴OC=BD=2,
而BD⊥x轴,
∴D点坐标为(4,2);
(3)解:OE+CE=AC.理由如下:
∵∠OAB=∠OBA=45°,
而∠DBO=90°,
∴∠DBE=45°,
在△BCE和△BDE
$\left\{\begin{array}{l}{BC=BD}\\{∠CBE=∠DBE}\\{BE=BE}\end{array}\right.$,
∴△BCE≌△BDE,
∴CE=DE,
∵△AOC≌△OBD,
∴AC=OD,
而OE+DE=OD,
∴OE+CE=AC.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

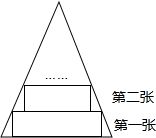 如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )| A. | 第4张 | B. | 第5张 | C. | 第6张 | D. | 第7张 |
| A. | 扩大10倍 | B. | 不变 | C. | 扩大5倍 | D. | 缩小5倍 |
| A. | (-2,-3) | B. | (3,-2) | C. | (2,3) | D. | (2,-3) |