题目内容
20.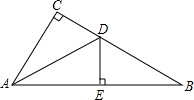 如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )
如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )| A. | AB=2AE | B. | AC=2CD | C. | DB=2CD | D. | AD=2DE |
分析 根据线段的垂直平分线的性质,等腰三角形的性质,角平分线的性质求出求出∠CAD=∠BAD=∠B=30°,根据30°角的直角三角形的性质即可判断.
解答 解:∵DE垂直平分AB,
∴AD=BD,AB=2AE,
∴∠DAB=∠B,
∵∠CAD=∠DAB=$\frac{1}{2}$∠BAC,
∴∠BAC=2∠B,
∵∠C=90°,
∴∠B=30°,∠BAC=60°,
∴∠CAD=∠DAB=30°,
∴AD=2CD,BD=AD=2DE,
∵AD是∠CAB的平分线,DC⊥AC,DE⊥AB,
∴DE=CD,
∴BD=2CD,
∵AD=2CD,AD>AC,
∴AC≠2CD,
故选B.
点评 本题考查了三角形的内角和定理,线段垂直平分线的性质,角平分线的性质,等腰三角形的判定,含30度角的直角三角形的性质的应用,注意:在直角三角形中,如果有一个角等于30°,那么它所对的直角边等于斜边的一半.

练习册系列答案
相关题目
10.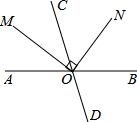 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=30°,则∠CON的度数为( )
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=30°,则∠CON的度数为( )
 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=30°,则∠CON的度数为( )
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=30°,则∠CON的度数为( )| A. | 30° | B. | 40° | C. | 60° | D. | 50° |
15.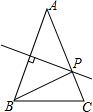 如图.△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=6cm,BC=4cm,△PBC的周长等于( )
如图.△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=6cm,BC=4cm,△PBC的周长等于( )
 如图.△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=6cm,BC=4cm,△PBC的周长等于( )
如图.△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=6cm,BC=4cm,△PBC的周长等于( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
5.用长为16m的木条围成一个矩形框架,设矩形面积为S(m2),则S的最大值为( )
| A. | 8m2 | B. | 16m2 | C. | 12m2 | D. | 32m2 |
12.下列计算正确的是( )
| A. | a3÷a2=a | B. | (-2a2)3=8a6 | C. | 2a2+a2=3a4 | D. | (a-b)2=a2-b2 |
 在美化校园的活动中,某兴趣小组想借助如图6所示的直角墙角(CD边所在的墙长10米,DA边所在的墙足够长),用28米长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x米.
在美化校园的活动中,某兴趣小组想借助如图6所示的直角墙角(CD边所在的墙长10米,DA边所在的墙足够长),用28米长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x米.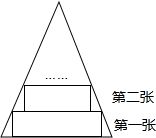 如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )