题目内容
8. 如图,在一次军演中,一艘潜艇在海面以下600米的点A处测得仰角为30°的正前方海面上C处有一艘可疑军舰,潜艇在同一深度以300$\sqrt{3}$米/分的速度直线航行20分钟到达点B处.测得该军舰在仰角为60°正前方的海面上D处.求军舰的平均速度.(精确到米,参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732,$\sqrt{5}$=2.236)
如图,在一次军演中,一艘潜艇在海面以下600米的点A处测得仰角为30°的正前方海面上C处有一艘可疑军舰,潜艇在同一深度以300$\sqrt{3}$米/分的速度直线航行20分钟到达点B处.测得该军舰在仰角为60°正前方的海面上D处.求军舰的平均速度.(精确到米,参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732,$\sqrt{5}$=2.236)
分析 过C作CE⊥AB于E,过D作DF⊥AB交AB的延长线于F,于是得到CE=DF=600,EF=CD,在Rt△ACE中求得AE=$\frac{CE}{tan30°}$=600$\sqrt{3}$,在RtDBF中,求得BF=$\frac{DF}{tan60°}$=200$\sqrt{3}$,即可得到结论.
解答  解:过C作CE⊥AB于E,过D作DF⊥AB交AB的延长线于F,
解:过C作CE⊥AB于E,过D作DF⊥AB交AB的延长线于F,
则CE=DF=600,EF=CD,
在Rt△ACE中,∵∠A=30°,
∴AE=$\frac{CE}{tan30°}$=600$\sqrt{3}$,
在RtDBF中,∵∠DBF=60°,
∴BF=$\frac{DF}{tan60°}$=200$\sqrt{3}$,
∵AB=300$\sqrt{3}$×20=6000$\sqrt{3}$,
∴CD=EF=5600$\sqrt{3}$,
∴军舰的平均速度=5600$\sqrt{3}$÷20≈48米/分.
点评 此题主要考查了仰角的定义及其解直角三角形的应用,解题时首先正确理解仰角的定义,然后利用三角函数和已知条件构造方程解决问题.

练习册系列答案
相关题目
3.在下列数中是方程x2+4x-5=0的解的是( )
| A. | -1 | B. | 5 | C. | 4 | D. | -5 |
 如图,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F,若CF平分AD,AB=2,求CD的长.
如图,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F,若CF平分AD,AB=2,求CD的长. 已知等腰梯形ABCD中,AD=3cm,BC=11cm,腰AB=5cm,点A为圆心,AD为半径的⊙A与底BC有怎样的位置关系?并说明理由.
已知等腰梯形ABCD中,AD=3cm,BC=11cm,腰AB=5cm,点A为圆心,AD为半径的⊙A与底BC有怎样的位置关系?并说明理由.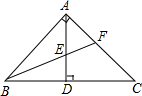 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BF交AD于点E,交AC于点F,且AE=AF,求证:BF平分∠ABC.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BF交AD于点E,交AC于点F,且AE=AF,求证:BF平分∠ABC. 点E是正方形ABCD的对角线BD上一点.∠AEF=90°,F在BC上,连接EC.求证:EF=EC.
点E是正方形ABCD的对角线BD上一点.∠AEF=90°,F在BC上,连接EC.求证:EF=EC. 如图,已知AB=AD,且AC平分∠BAD,求证:BC=DC.
如图,已知AB=AD,且AC平分∠BAD,求证:BC=DC.