题目内容
19.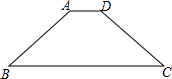 已知等腰梯形ABCD中,AD=3cm,BC=11cm,腰AB=5cm,点A为圆心,AD为半径的⊙A与底BC有怎样的位置关系?并说明理由.
已知等腰梯形ABCD中,AD=3cm,BC=11cm,腰AB=5cm,点A为圆心,AD为半径的⊙A与底BC有怎样的位置关系?并说明理由.
分析 作AM⊥BC于M,DN⊥BC于N,则∠AMB=∠DNC=90°,MN=AD=3,MB=CN=$\frac{1}{2}$(BC-AD)=4,由勾股定理得出AM=3,得出AM=AD,即d=r,即可得出结论.
解答 解:点A为圆心,AD为半径的⊙A与底BC相切;理由如下:
作AM⊥BC于M,DN⊥BC于N,如图所示:
则∠AMB=∠DNC=90°,MN=AD=3,MB=CN=$\frac{1}{2}$(BC-AD)=4,
由勾股定理得:AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AM=AD,即d=r,
∴⊙A与底BC相切.
点评 本题考查了直线与圆的位置关系、等腰梯形的性质、勾股定理、矩形的性质;熟练掌握等腰梯形的性质,由勾股定理求出AM是解决问题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
11.图①所示的是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间的小三角形三边的中点,得到图③,按此方法继续连接,请你根据每个图中三角形的个数的规律完成各题:
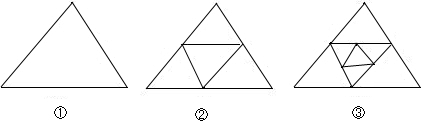
(1)将下表填写完整;
(2)在第n个图形中有4n-3个三角形;(用含n的式子表示)
(3)按照上述方法,能否得到2017个三角形?如果能,请求出n;如果不能,请简述理由.

(1)将下表填写完整;
| 图形编号 | ① | ② | ③ | ④ | ⑤ | … |
| 三角形个数 | 1 | 5 | 9 | 13 | 17 | … |
(3)按照上述方法,能否得到2017个三角形?如果能,请求出n;如果不能,请简述理由.
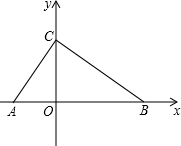 已知:在平面直角坐标系中,点O为坐标原点,△ABC的顶点A(-2,0),点B、C分别在x轴正半轴上和y轴正半轴上,∠ACB=90°,∠BAC=60°.
已知:在平面直角坐标系中,点O为坐标原点,△ABC的顶点A(-2,0),点B、C分别在x轴正半轴上和y轴正半轴上,∠ACB=90°,∠BAC=60°. 如图,在一次军演中,一艘潜艇在海面以下600米的点A处测得仰角为30°的正前方海面上C处有一艘可疑军舰,潜艇在同一深度以300$\sqrt{3}$米/分的速度直线航行20分钟到达点B处.测得该军舰在仰角为60°正前方的海面上D处.求军舰的平均速度.(精确到米,参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732,$\sqrt{5}$=2.236)
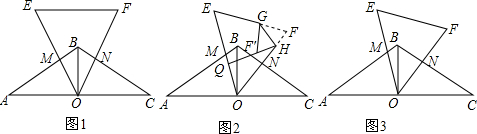
如图,在一次军演中,一艘潜艇在海面以下600米的点A处测得仰角为30°的正前方海面上C处有一艘可疑军舰,潜艇在同一深度以300$\sqrt{3}$米/分的速度直线航行20分钟到达点B处.测得该军舰在仰角为60°正前方的海面上D处.求军舰的平均速度.(精确到米,参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732,$\sqrt{5}$=2.236)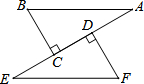 如图,AB=EF,BC⊥AE于C,FD⊥AE于D,CE=DA.求证:
如图,AB=EF,BC⊥AE于C,FD⊥AE于D,CE=DA.求证: