题目内容
17．计算$\sqrt{1+ta{n}^{2}7°}•sin83°$=1．分析 sin83°=cos7°．然后将括号外的cos7°移到括号内，接下来再化简计算即可．
解答 解：原式=$\sqrt{1+ta{n}^{2}7°}•cos7°$=$\sqrt{（1+\frac{si{n}^{2}7°}{co{s}^{2}7°}）•co{s}^{2}7°}$=$\sqrt{co{s}^{2}7°+si{n}^{2}7°}$=1．
故答案为：1．
点评 本题主要考查的是同角三角函数的关系，互余两角三角函数的关系，掌握相关性质是解题的关键．
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
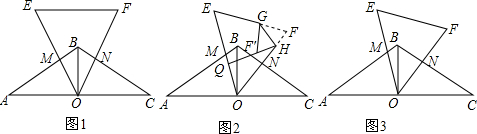
如图，在一次军演中，一艘潜艇在海面以下600米的点A处测得仰角为30°的正前方海面上C处有一艘可疑军舰，潜艇在同一深度以300$\sqrt{3}$米/分的速度直线航行20分钟到达点B处．测得该军舰在仰角为60°正前方的海面上D处．求军舰的平均速度．（精确到米，参考数据：$\sqrt{2}$=1.414，$\sqrt{3}$=1.732，$\sqrt{5}$=2.236）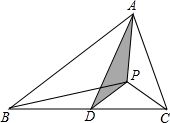
如图，△ABC中，D是BC边的中点，已知点P是△ACD内一点，己知△ACP的面积为7，△ABP的面积为13，则阴影部分的面积为3．
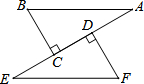如图，AB=EF，BC⊥AE于C，FD⊥AE于D，CE=DA．求证：
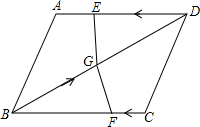如图，在四边形ABCD中，AD=BC=4，AB=CD，BD=6，点E从D点出发，以每秒1个单位的速度沿DA向点A匀速移动，点F从点C出发，以每秒3个单位的速度沿C→B→C作匀速移动，点G从点B出发沿BD向点D匀速移动，三个点同时出发，当有一个点到达终点时，其余两点也随之停止运动．