题目内容
20.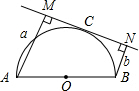 如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )
如图,AB是半圆O的直径,直线MN切半圆于点C,且AM⊥MN于M,BN⊥MN于N,如果AM=a,BN=b,则半圆O的半径为( )| A. | $\frac{3}{2}$(a+b) | B. | (a+b) | C. | $\frac{1}{2}$(a+b) | D. | $\frac{1}{3}$(a+b) |
分析 根据切线的性质,只需连接OC.根据切线的性质定理以及平行线等分线段定理得到梯形的中位线,再根据梯形的中位线定理进行计算即可.
解答  解:连接OC,则OC⊥MN.
解:连接OC,则OC⊥MN.
∴OC∥AM∥BN,
又OA=OB,
∴MC=NC.
根据梯形的中位线定理,得该半圆的半径是$\frac{a+b}{2}$,
则该圆的直径为(a+b),
∴半圆O的半径为$\frac{1}{2}$(a+b),
故选C.
点评 此题主要考查了切线的性质定理和平行线等分线段定理,梯形的中位线,熟练运用梯形的中位线定理求解是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
10.$\frac{1}{2016}$的倒数是( )
| A. | 2016 | B. | $\frac{1}{2016}$ | C. | -2016 | D. | -$\frac{1}{2016}$ |
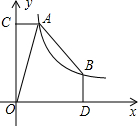 在平面直角坐标系xOy中,A,B两点在函数C1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,其中k1>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1.
在平面直角坐标系xOy中,A,B两点在函数C1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,其中k1>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1. 如图,抛物线y=x2上的三点A、B、C的横坐标分别为a-d、a、a+d,试求△ABC的面积(用含有a,d的代数式表示).
如图,抛物线y=x2上的三点A、B、C的横坐标分别为a-d、a、a+d,试求△ABC的面积(用含有a,d的代数式表示).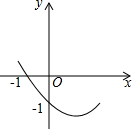 如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.
如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.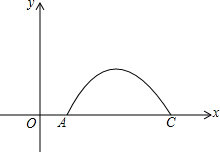 如图,一大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx+c,小王骑自行车从O匀速沿直线到拱梁一端A,再匀速通过拱梁部分的桥面AC,小王从O到A用了2秒,当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小王骑自行车通过拱梁部分的桥面AC供需26秒.
如图,一大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx+c,小王骑自行车从O匀速沿直线到拱梁一端A,再匀速通过拱梁部分的桥面AC,小王从O到A用了2秒,当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小王骑自行车通过拱梁部分的桥面AC供需26秒.