题目内容
2. 如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言,$\widehat{MTN}$的度数为( )
如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆交AC、BC于M、N,则对于所有可能的圆的位置而言,$\widehat{MTN}$的度数为( )| A. | 从30°到60°变动 | B. | 从60°到90°变动 | C. | 保持30°不变 | D. | 保持60°不变 |
分析 过点O作OH∥AC,交AB与点H,交BC于点Z,过点O作OE∥BC,交AB的延长线于点E,连接OM,ON,过点M作MG⊥OH于点G,作NK⊥OE于点K,根据△ACB是等边三角形可知∠A=∠ACB=∠ABC=60°,故可判断出∠HOE=60°,再由HL定理得出△OMG≌△ONK,故可得出∠MOG=∠KON,故∠MON=60°,由此可得出结论.
解答  解:过点O作OH∥AC,交AB与点H,交BC于点Z,过点O作OE∥BC,交AB的延长线于点E,连接OM,ON,过点M作MG⊥OH于点G,作NK⊥OE于点K,
解:过点O作OH∥AC,交AB与点H,交BC于点Z,过点O作OE∥BC,交AB的延长线于点E,连接OM,ON,过点M作MG⊥OH于点G,作NK⊥OE于点K,
∵△ACB是等边三角形,
∴∠A=∠ACB=∠ABC=60°.
∵OE∥BC,
∴∠ACB=∠CZO=60°.
∴∠HZB=60°.
∵OE∥CB,
∴∠EOH=∠HZB=60°.
∵OC∥AB,
∴四边形AHOC是平行四边形,
∴∠A=∠COZ=60°,
∴△OZC是等边三角形,
∵MG⊥OH,NK⊥OH,
∴MG,NK均为△OZC的高,
∴MG=NK.
在Rt△OMG与Rt△ONK中,
∵$\left\{\begin{array}{l}OM=ON\\ MG=NK\end{array}\right.$,
∴△OMG≌△ONK(HL),
∴∠MOG=∠KON,
∴∠MON=60°,
∴$\widehat{MTN}$的度数为60°.
故选D.
点评 本题考查的是切线的性质,根据题意作出辅助线,构造出平行四边形及等边三角形,利用圆心角与弧的关系求解是解答此题的关键.

练习册系列答案
相关题目

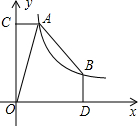 在平面直角坐标系xOy中,A,B两点在函数C1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,其中k1>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1.
在平面直角坐标系xOy中,A,B两点在函数C1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,其中k1>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1.