Question

16．如图1，直线AB∥CD，点P在两平行线之间，点E在AB上，点F在CD上，连结PE，PF．
（1）若∠PEB=60°，∠PFD=50°，请求出∠EPF．（请写出必要的步骤说明理由）

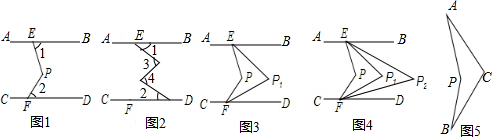
（2）如图2，若点P、Q在直线AB与CD之间时，∠1=30°，∠2=40°，∠3=70°，请求出∠4=80°．（不需说明理由，请直接写出答案）
（3）如图3，在图1基础上，作P₁E平分∠PEB，P₁F平分∠PFD，若设∠PEB=x°，∠PFD=y°．则∠P₁=$\frac{1}{2}$（x+y）°（用x，y的代数式表示），若P₂E平分∠P₁EB，P₂F平分∠P₁FD，可得∠P₂，P₃E平分∠P₂EB，P₃F平分∠P₂FD，可得∠P₃…，依次平分下去，则∠P_n=（$\frac{1}{2}$）ⁿ（x+y）°．
（4）在一次综合实践活动课上，张开同学制作了一个图5的“回旋镖”，经测量发现∠PAC=38°，∠PBC=22°，他很想知道∠APB与∠C的数量关系，你能告诉他吗？请你直接写出答案：∠APB=∠C+60°．

Answer 1

分析 （1）过点P作PH∥AB∥CD，根据平行线的性质：两直线平行，内错角相等即可证得；
（2）同理依据两直线平行，内错角相等即可证得∠1+∠4=∠2+∠3，求得∠4=80°；
（3）利用（1）的结论和角平分线的性质即可写出结论；
（4）过A、B分别作直线AE、BF，使AE∥BF，利用（1）的结论即可求解．

解答 解：（1）如图1，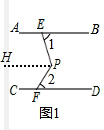

过点P作PH∥AB∥CD
∴∠1=∠EPH，∠2=∠FPH
而∠EPF=∠EPH+∠FPH
∴∠EPF=∠1+∠2=110°；
（2）∠4=80°，（3）∠P₁=$\frac{1}{2}$（x+y）°（用x，y的代数式表示）
∠P_n=（$\frac{1}{2}$）ⁿ（x+y）°．
（4）∠APB=∠C+60°．理由如下：
过A、B分别作直线AE、BF，使AE∥BF．如图，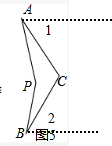

由（1）规律可知∠C=∠1+∠2．
∠APB=∠PAE+∠PBF
=（∠PAC+∠1）+（∠PBC+∠2）
=∠PAC+∠PBC+（∠1+∠2）
=∠C+60°．

点评 本题考查了平行线性质的应用，关键是正确作辅助线，利用性质解决问题．