题目内容
7．某组数据的方差计算公式为S2=$\frac{1}{20}$[（x1-6）2+（x2-6）2+…+（x20-6）2]，则该组数据的样本容量是20，该组数据的平均数是6．分析 方差公式S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]中，n表示样本容量，x1，x2，…xn表示样本数据，平均数为$\overline{x}$．
解答 解：某组数据的方差计算公式为S2=$\frac{1}{20}$[（x1-6）2+（x2-6）2+…+（x20-6）2]，则该组数据的样本容量是20，该组数据的平均数是6，
故答案为：20；6．
点评 此题主要考查了方差公式，关键是差的定义：一般地设n个数据，x1，x2，…xn的平均数为$\overline{x}$，则方差S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．
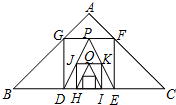如图，已知在Rt△ABC中，AB=AC=2，在△ABC内作第一个内接正方形DEFG；然后取GF的中点P，连接PD、PE，在△PDE内作第二个内接正方形HIKJ；再取线段KJ的中点Q，在△QHI内作第三个内接正方形…依次进行下去，则第n个内接正方形的边长为（ ）
如图，已知在Rt△ABC中，AB=AC=2，在△ABC内作第一个内接正方形DEFG；然后取GF的中点P，连接PD、PE，在△PDE内作第二个内接正方形HIKJ；再取线段KJ的中点Q，在△QHI内作第三个内接正方形…依次进行下去，则第n个内接正方形的边长为（ ）| A． | $\frac{2}{3}•{（\frac{1}{2}）^{n-1}}$ | B． | $\frac{{2\sqrt{2}}}{3}•{（\frac{1}{2}）^{n-1}}$ | C． | $\frac{2}{3}•{（\frac{1}{2}）^n}$ | D． | $\frac{{2\sqrt{2}}}{3}•{（\frac{1}{2}）^n}$ |
2．已知关于x的一元二次方程（m-1）x2+x+m2+4m-5=0的一个根为0，则m的值为（ ）
| A． | 1 | B． | -5 | C． | 1或-5 | D． | m≠1的任意实数 |
