题目内容
18.阅读材料后解决问题:小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)(22+1)(24+1)(28+1)
=(2+1)(2-1)(22+1)(24+1)(28+1)
=(22-1)(22+1)(24+1)(28+1)
=(24-1)(24+1)(28+1)
=(28-1)(28+1)
=216-1
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1)=232-1.
(2)(3+1)(32+1)(34+1)(38+1)(316+1)=$\frac{{{3^{32}}-1}}{2}$.
(3)化简:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
分析 (1)原式变形后,利用题中的规律计算即可得到结果;
(2)原式变形后,利用题中的规律计算即可得到结果;
(3)分m=n与m≠n两种情况,化简得到结果即可.
解答 解:(1)原式=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)=232-1;
故答案为:232-1
(2)原式=$\frac{1}{2}$(3-1)(3+1)(32+1)(34+1)(38+1)(316+1)=$\frac{{{3^{32}}-1}}{2}$;
故答案为:$\frac{{3}^{32}-1}{2}$;
(3)(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
当m≠n时,原式=$\frac{1}{m-n}$(m-n)(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16)=$\frac{{{m^{32}}-{n^{32}}}}{m-n}$;
当m=n时,原式=2m•2m2…2m16=32m31.
点评 此题考查了平方差公式,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
8.下列运算不正确的是( )
| A. | 2a3÷a=2a2 | B. | ($\sqrt{2}$-1)0=0 | C. | $\root{3}{8}$=2 | D. | (ab2)2=a2b4 |
6.-$\frac{2016}{2015}$的倒数是( )
| A. | $\frac{2016}{2015}$ | B. | -$\frac{2016}{2015}$ | C. | $\frac{2015}{2016}$ | D. | -$\frac{2015}{2016}$ |
13.下列计算结果正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a6 | C. | (a3)2=a9 | D. | a6÷a2=a3 |
10.下列计算正确的是( )
| A. | $\sqrt{6}-\sqrt{3}=\sqrt{3}$ | B. | $\sqrt{6}÷\sqrt{3}=\sqrt{2}$ | C. | $\sqrt{{{(-3)}^2}}=-3$ | D. | $\sqrt{9}=±3$ |
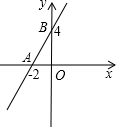 如图,直线y=kx+b经过A、B两点.
如图,直线y=kx+b经过A、B两点. 如图,在矩形ABCD中,AD=4,AB=3,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是6.
如图,在矩形ABCD中,AD=4,AB=3,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是6.