题目内容
9.先化简,再求代数式的值.($\frac{3}{a+1}$-$\frac{a-3}{{a}^{2}-1}$)÷$\frac{a}{a-1}$,其中-2≤a≤1且a为整数,请你取一个合适的数作为a的值代入求值.
分析 先将题目中的式子化简,然后选取合适的a的值代入即可解答本题.
解答 解:($\frac{3}{a+1}$-$\frac{a-3}{{a}^{2}-1}$)÷$\frac{a}{a-1}$
=$\frac{3(a-1)-(a-3)}{(a+1)(a-1)}×\frac{a-1}{a}$
=$\frac{3a-3-a+3}{(a+1)(a-1)}×\frac{a-1}{a}$
=$\frac{2a}{(a+1)(a-1)}×\frac{a-1}{a}$
=$\frac{2}{a+1}$,
当a=-2时,
原式=$\frac{2}{-2+1}=-2$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法,注意选取的a值要使得原分式有意义.

练习册系列答案
相关题目
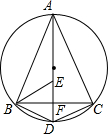 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.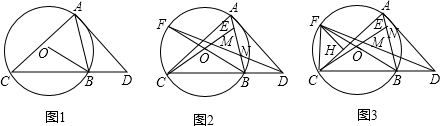
 尺规作图:已知∠α,求作:∠A使∠A=∠α( 不写作法,保留痕迹 )
尺规作图:已知∠α,求作:∠A使∠A=∠α( 不写作法,保留痕迹 )