题目内容
14.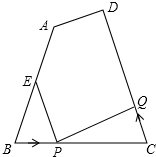 如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等?请说明理由.
(2)当点Q的运动速度为多少时,能够使△BPE与△CQP全等.
分析 (1)经过1秒后,可得BP=CQ=3,则PC=8-3=5,可证明△BPE≌△CQP;
(2)由△BPE与△CQP全等可知有△BEP≌△CQP或△BEP≌△CPQ,全等可得BP=CP或BP=CQ,或可求得BP的长,可求得P点运动的时间,由CQ=BE或CQ=BP可求得Q点运动的路程,可求得其速度.
解答 解:
(1)全等,理由如下:
当运动1秒后,则BP=CQ=3cm,
∴PC=BC-BP=8cm-3cm=5cm,
∵E为AB中点,且AB=10cm
∴BE=5cm,
∴BE=PC,
在△BPE和△CQP中
$\left\{\begin{array}{l}{BE=PC}\\{∠B=∠C}\\{BP=CQ}\end{array}\right.$
∴△BPE≌△CQP(SAS);
(2)∵△BPE与△CQP全等,
∴有△BEP≌△CQP或△BEP≌△CPQ,
当△BEP≌△CQP时,
则BP=CP,CQ=BE=5cm,
设P点运动的时间为t秒,
则3t=8-3t,解得t=$\frac{4}{3}$秒,
∴Q点的速度=5÷$\frac{4}{3}$=$\frac{15}{4}$(cm),
当△BEP≌△CPQ时,
由(1)可知t=1(秒),
∴BP=CQ=3,
∴Q点的速度=3÷1=3(cm),
即当Q点每秒运动$\frac{15}{4}$cm或3cm时△BEP≌△CQP.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定是解题的关键,即SSS、SAS、ASA、AAS和HL

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
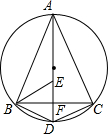 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD. 求如图4×4方格中线段AE,BC,CD的长.
求如图4×4方格中线段AE,BC,CD的长.