题目内容
19．
已知：如图，直线AB，CD被直线EF所截，AB∥CD，交点分别为G、H，射线GM平分∠EGB，射线HN平分∠EHD．求证：GM∥BN．
分析 先根据平行线的性质，得出∠BGE=∠DHG，再根据角平分线的定义，得出∠EGM=∠GHN，进而得到GM∥BN．
解答 证明：∵AB∥CD，
∴∠BGE=∠DHG，
又∵射线GM平分∠EGB，射线HN平分∠EHD，
∴∠EGM=∠GHN，
∴GM∥BN．
点评 本题主要考查了平行线的性质与判定，应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
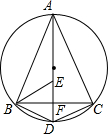如图，AD为△ABC外接圆的直径，AD⊥BC，垂足为点F，∠ABC的平分线交AD于点E，连接BD，CD．
推理填空：