题目内容
19.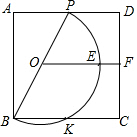 如图,正方形ABCD的边长为4,点P为线段AD上的一动点(不与点A、D重合),以BP为直径作半圆,圆心为点O,半圆O边BC交于点K,线段OF∥AD,且与CD相交于点F,与半圆O相交于点E,设AP=x.
如图,正方形ABCD的边长为4,点P为线段AD上的一动点(不与点A、D重合),以BP为直径作半圆,圆心为点O,半圆O边BC交于点K,线段OF∥AD,且与CD相交于点F,与半圆O相交于点E,设AP=x.(1)当x为何值时,四边形OBKE为菱形;
(2)当半圆O与CD相切时,试求x的值.
分析 (1)连接PK,当OE=BK时,四边形OBKE是菱形,据此即可列方程求得;
(2)当半圆O与CD相切时,延长EO与AB相交于M,在Rt△OBM中,根据勾股定理可求解.
解答 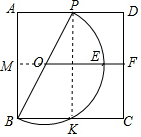 解:(1)连接PK.
解:(1)连接PK.
∵BP是直径,
∴∠BKP=90°,
∵在正方形ABCD中,∠A=∠ABC=90°,
∴四边形ABKP是矩形,
∴BK=AP=x,
又AB=4,
∴BP=$\sqrt{{4}^{2}+{x}^{2}}$=$\sqrt{16+{x}^{2}}$.
∵OF∥BC,OE=OB,
∴当OE=BK时,四边形OBKE是菱形.
此时$\frac{1}{2}$$\sqrt{16+{x}^{2}}$=x,
∵x>0,
∴x=$\frac{4\sqrt{3}}{3}$;
(2)如图,当半圆O与CD相切时,
延长EO与AB相交于M.
∵OF∥AD,
∴OF⊥CD,
∴此时点E与点F重合.
∵OF∥AD,且O是BP的中点,
∴BM=2,OM=$\frac{x}{2}$.
∴OE=OF=4-$\frac{x}{2}$.
在Rt△OBM中,根据勾股定理可得4+($\frac{x}{2}$)2=(4-$\frac{x}{2}$)2,
解得x=3,即AP=3时,半圆O与CD相切.
点评 本题考查了圆的综合题:熟练掌握圆的切线的判定定理、菱形的判定方法、正方形的性质;会运用勾股定理进行几何计算.

练习册系列答案
相关题目
9. 若数字a的位置如图所示,化简|1+a|+|2-a|得( )
若数字a的位置如图所示,化简|1+a|+|2-a|得( )
 若数字a的位置如图所示,化简|1+a|+|2-a|得( )
若数字a的位置如图所示,化简|1+a|+|2-a|得( )| A. | 1 | B. | -2a+1 | C. | 2a+1 | D. | 3 |
7.已知△ABC~△DEF,相似比为3:1,且△ABC的面积与△DEF的面积和为20,则△DEF的面积为( )
| A. | 5 | B. | 2 | C. | 15 | D. | 18 |
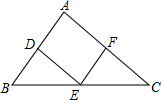 如图,在△ABC中,已知D、E、F分别是AB、BC、CA的中点.
如图,在△ABC中,已知D、E、F分别是AB、BC、CA的中点.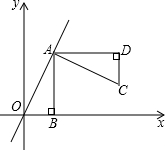 如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B.
如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B.