题目内容
11.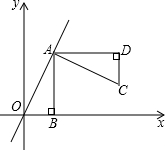 如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B.
如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B.(1)求该正比例函数的解析式;
(2)将△ABO绕点A逆时针旋转90°得到△ADC,求点C的坐标;
(3)试判断点C是否在直线y=$\frac{1}{3}$x+1的图象上,说明你的理由.
分析 (1)将点A(2,4)代入y=kx,利用待定系数法即可求出该正比例函数的解析式;
(2)先由AB⊥x轴于点B,且A(2,4),得出OB=2,AB=4.再根据旋转的性质得出AD=AB=4,DC=OB=2,即D点横坐标为6,C点纵坐标是2,进而求出点C的坐标;
(3)把点C的坐标(6,2)代入y=$\frac{1}{3}$x+1,即可判断.
解答 解:(1)∵正比例函数y=kx经过点A(2,4),
∴2k=4,解得k=2,
∴该正比例函数的解析式为y=2x;
(2)∵AB⊥x轴于点B,且A(2,4),
∴OB=2,AB=4.
∵将△ABO绕点A逆时针旋转90°得到△ADC,
∴AD=AB=4,DC=OB=2,
∴D点横坐标为6,C点纵坐标是2,
∴点C的坐标为(6,2);
(3)把点C的坐标(6,2)代入y=$\frac{1}{3}$x+1,
得左边=2,右边=$\frac{1}{3}$×6+1=3,
左边≠右边,
即点C不在直线y=$\frac{1}{3}$x+1的图象上.
点评 本题考查了待定系数法求正比例函数的解析式,旋转的性质,一次函数图象上点的坐标特征,是基础知识,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若a<b,则下列不等式一定成立的是( )
| A. | $\frac{b}{a}$>1 | B. | $\frac{a}{b}$<1 | C. | -a>-b | D. | a-b>0 |
20.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{11}$ | D. | $\sqrt{20}$ |
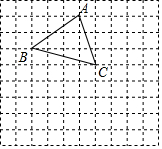 在边长为1的正方形网格中,△ABC的位置如图所示:
在边长为1的正方形网格中,△ABC的位置如图所示: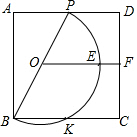 如图,正方形ABCD的边长为4,点P为线段AD上的一动点(不与点A、D重合),以BP为直径作半圆,圆心为点O,半圆O边BC交于点K,线段OF∥AD,且与CD相交于点F,与半圆O相交于点E,设AP=x.
如图,正方形ABCD的边长为4,点P为线段AD上的一动点(不与点A、D重合),以BP为直径作半圆,圆心为点O,半圆O边BC交于点K,线段OF∥AD,且与CD相交于点F,与半圆O相交于点E,设AP=x.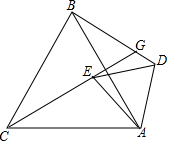 如图,△ABC、△ADE都是等边三角形,点G为射线BD,CE的交点.
如图,△ABC、△ADE都是等边三角形,点G为射线BD,CE的交点.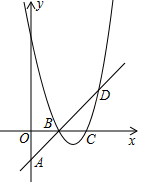 已知抛物线y=ax2+bx+8(a≥1)过点D(5,3),与x轴交于点B、C(点B、C均在y轴右侧)且BC=2,直线BD交y轴于点A.
已知抛物线y=ax2+bx+8(a≥1)过点D(5,3),与x轴交于点B、C(点B、C均在y轴右侧)且BC=2,直线BD交y轴于点A.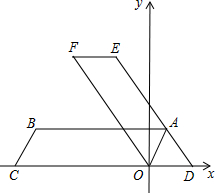 如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将?ABCO绕点O顺时针旋转α°(0<α<90°)得到?DEFO,点A的对应点点D恰好落在x轴的正半轴上,且DE经过点A.
如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将?ABCO绕点O顺时针旋转α°(0<α<90°)得到?DEFO,点A的对应点点D恰好落在x轴的正半轴上,且DE经过点A.