��Ŀ����
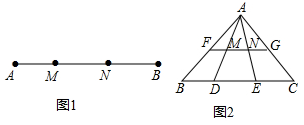
8�����壺��ͼ1����M��N���߶�AB�ָ��AM��MN��BN������AM��MN��BNΪ�ߵ���������һ��ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɷָ�㣮�����������⣺
��1����֪��M��N���߶�AB�Ĺ��ɷָ�㣬��BN��MN��AM����AM=2��MN=3����BN�ij���
��2����ͼ2������F��M��N��G�ֱ���AB��AD��AE��AC���ϵ��е㣬��D��E���߶�BC�Ĺ��ɷָ�㣬��EC��DE��BD����֤����M��N���߶�FG�Ĺ��ɷָ�㣮
���� ��1����M��NΪ�߶�AB�Ĺ��ɷָ�㣬�������е��¶����г���ϵʽ����MN��AM�ij��������BN�ij����ɣ�
��2����F��M��N��G�ֱ�Ϊ�����е㣬�õ�FM��MN��NG�ֱ�Ϊ��λ�ߣ�������λ�߶����õ�BD=2FM��DE=2MN��EC=2NG�������������¶����г���ϵʽ�����ɵ�֤��
��� ��1����ߵ�M��N���߶�AB�Ĺ��ɷָ�㣬��BN��MN��AM��AM=2��MN=3��
��BN2=MN2+AM2=9+4=13��
��BN=$\sqrt{13}$��
��2��֤���ߵ�F��M��N��G�ֱ���AB��AD��AE��AC���ϵ��е㣬
��FM��MN��NG�ֱ��ǡ�ABD����ADE����AEC����λ�ߣ�
��BD=2FM��DE=2MN��EC=2NG��
�ߵ�D��E���߶�BC�Ĺ��ɷָ�㣬��EC��DE��BD��
��EC2=DE2+DB2��
��4NG2=4MN2+4FM2��
��NG2=MN2+FM2��
���M��N���߶�FG�Ĺ��ɷָ�㣮
���� ���⿼���˹��ɶ�����Ū�����е��¶����ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
20�����ж��θ�ʽ�����������θ�ʽ���ǣ�������
| A�� | $\sqrt{24}$ | B�� | $\sqrt{36}$ | C�� | $\sqrt{11}$ | D�� | $\sqrt{20}$ |
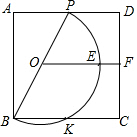 ��ͼ��������ABCD�ı߳�Ϊ4����PΪ�߶�AD�ϵ�һ���㣨�����A��D�غϣ�����BPΪֱ������Բ��Բ��Ϊ��O����ԲO��BC���ڵ�K���߶�OF��AD������CD�ཻ�ڵ�F�����ԲO�ཻ�ڵ�E����AP=x��
��ͼ��������ABCD�ı߳�Ϊ4����PΪ�߶�AD�ϵ�һ���㣨�����A��D�غϣ�����BPΪֱ������Բ��Բ��Ϊ��O����ԲO��BC���ڵ�K���߶�OF��AD������CD�ཻ�ڵ�F�����ԲO�ཻ�ڵ�E����AP=x��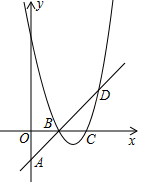 ��֪������y=ax2+bx+8��a��1������D��5��3������x�ύ�ڵ�B��C����B��C����y���Ҳࣩ��BC=2��ֱ��BD��y���ڵ�A��
��֪������y=ax2+bx+8��a��1������D��5��3������x�ύ�ڵ�B��C����B��C����y���Ҳࣩ��BC=2��ֱ��BD��y���ڵ�A��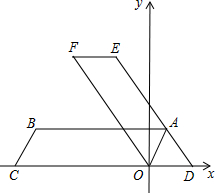 ��ͼ���ı���ABCO��ƽ���ı��Σ�OA=2��AB=6����C��x��ĸ������ϣ���?ABCO�Ƶ�O˳ʱ����ת���㣨0������90�㣩�õ�?DEFO����A�Ķ�Ӧ���Dǡ������x����������ϣ���DE������A��
��ͼ���ı���ABCO��ƽ���ı��Σ�OA=2��AB=6����C��x��ĸ������ϣ���?ABCO�Ƶ�O˳ʱ����ת���㣨0������90�㣩�õ�?DEFO����A�Ķ�Ӧ���Dǡ������x����������ϣ���DE������A��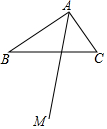 ��ͼ����Rt��ABC�У���BAC=90�㣬AB��AC������AMƽ�֡�BAC��
��ͼ����Rt��ABC�У���BAC=90�㣬AB��AC������AMƽ�֡�BAC��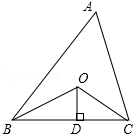 ��ͼ����֪��ABC�������20��OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��OD��BC��D����OD=3�����ABC���ܳ���$\frac{40}{3}$��
��ͼ����֪��ABC�������20��OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��OD��BC��D����OD=3�����ABC���ܳ���$\frac{40}{3}$��