题目内容
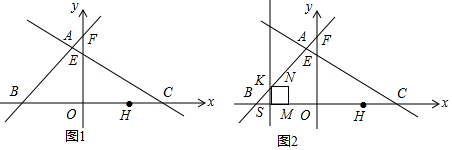
14.如图(1),在平面直角坐标系中,直线AB、AC分别与x轴相交于点B、C,tan∠ACB=$\frac{3}{5}$,直线AB的解析式为y=x+7,AC与y轴交于点E(0,$\sqrt{34}$),AB与y轴交于点F.(1)直接填空:直线AC的函数解析式为y=-$\frac{3}{5}$x+$\sqrt{34}$,原点O到直线AC的距离=5;
(2)如图2,平行于y轴的直线1从点B出发,沿x轴向终点O移动,速度为1单位/秒,移动过程中直线1分别与直线AB和x轴交于点K、S,以KS为一边,作正方形KSMN,使该正方形与原点O在直线l的同侧,设移动时间为t,求出正方形KSMN与△ABC重叠部分的面积S与移动的时间t的函数关系式,并写出自变量的取值范围;
(3)已知点H(5,0),在△ABC的边上取两点P,Q,是否存在O,P,Q为顶点的三角形与△OHP全等,且这两个三角形在OP的异侧?若存在,请直接写出所有符合题意的点P的坐标;若不存在,请说明理由.
分析 (1)根据三角函数先求OC的长,写出C的坐标,利用待定系数法求直线AC的解析式,作垂线段OG,利用三角函数求OG的长即可;
(2)分三种情况:
①先计算当N在直线AC上时,如图4,求出t的值;当0≤t≤$\frac{21+5\sqrt{34}}{11}$时,如图3,正方形KSMN与△ABC重叠部分的面积是正方形KSMN,②当K与A重合时,如图5,求出此时t的值,当$\frac{21+5\sqrt{34}}{11}$<t≤$\frac{21+5\sqrt{34}}{8}$时,如图6,正方形KSMN与△ABC重叠部分的面积是五边形GKSMH的面积,③当$\frac{21+5\sqrt{34}}{8}$<t≤7时,如图7,设KS与AC交于G,MN于AC交于H,则正方形KSMN与△ABC重叠部分的面积是梯形GSMH的面积,分别表示其面积S即可;
(3)存在两种情况:①通过观察可以发现Q点与点G重合,通过直线求出点P坐标即可.
②如图9,P与E重合,P的坐标就是点E的坐标.
解答  解:(1)如图1,∵E(0,$\sqrt{34}$),
解:(1)如图1,∵E(0,$\sqrt{34}$),
∴OE=$\sqrt{34}$,
Rt△OEC中,tan∠ACB=$\frac{3}{5}=\frac{OE}{OC}$,
∴$\frac{3}{5}=\frac{\sqrt{34}}{OC}$,
∴OC=$\frac{5\sqrt{34}}{3}$,
∴C($\frac{5\sqrt{34}}{3}$,0),
设直线AC的解析式为:y=kx+b,
把E(0,$\sqrt{34}$)和C($\frac{5\sqrt{34}}{3}$,0)代入得:$\left\{\begin{array}{l}{b=\sqrt{34}}\\{\frac{5\sqrt{34}}{3}k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{5}}\\{b=\sqrt{34}}\end{array}\right.$,
∴直线AC的解析式为:y=-$\frac{3}{5}$x+$\sqrt{34}$,
过O作OG⊥AC于G,
在Rt△OEC中,由勾股定理得:EC=$\sqrt{(\sqrt{34})^{2}+(\frac{5\sqrt{34}}{3})^{2}}$=$\frac{34}{3}$,
在Rt△OGC中,sin∠ACB=$\frac{OE}{EC}=\frac{OG}{OC}$,
∴$\frac{\sqrt{34}}{\frac{34}{3}}$=$\frac{OG}{\frac{5\sqrt{34}}{3}}$,
∴OG=5,
则原点O到直线AC的距离为5,
故答案为:y=-$\frac{3}{5}$x+$\sqrt{34}$;5;
(2)分三种情况:
当x=0时,y=7,
当y=0时,x=-7,
∴B(-7,0),F(0,7),
∴OB=OF=7,
∴△OBF是等腰直角三角形,
∴∠FBO=45°,
∵四边形KSMN是正方形,
∴∠KSM=90°,KS=SM,
∴△ASK是等腰直角三角形,
∴AS=KS=t,
当M与O重合时,如图2,
由AM=7得:2t=7,
t=3.5,
①当N在直线AC上时,如图4,
∴BS=KS=SM=t,
∴MC=OB+OC-2t=7+$\frac{5\sqrt{34}}{3}$-2t,
tan∠ACB=$\frac{3}{5}=\frac{MN}{MC}$,
∴$\frac{3}{5}$=$\frac{t}{7+\frac{5\sqrt{34}}{3}-2t}$,
t=$\frac{21+5\sqrt{34}}{11}$,
当0≤t≤$\frac{21+5\sqrt{34}}{11}$时,如图3,正方形KSMN与△ABC重叠部分的面积是正方形KSMN,
∴S=S正方形KSMN=t2,
②当K与A重合时,如图5,
则$\left\{\begin{array}{l}{y=x+7}\\{y=-\frac{3}{5}x+\sqrt{34}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{-35+5\sqrt{34}}{8}}\\{y=\frac{21+5\sqrt{34}}{8}}\end{array}\right.$,
∴t=BS=AS=$\frac{21+5\sqrt{34}}{8}$,
当$\frac{21+5\sqrt{34}}{11}$<t≤$\frac{21+5\sqrt{34}}{8}$时,如图6,正方形KSMN与△ABC重叠部分的面积是五边形GKSMH的面积,
MC=7+$\frac{5\sqrt{34}}{3}$-2t,
tan∠ACB=$\frac{MH}{CM}=\frac{3}{5}$,
∴MH=$\frac{3}{5}$CM=$\frac{3}{5}$(7+$\frac{5\sqrt{34}}{3}$-2t)=$\frac{21}{5}+\sqrt{34}-\frac{6}{5}t$,
∴NH=t-MH=$\frac{11}{5}t-\frac{21}{5}-\sqrt{34}$,
∵KN∥SM
∴∠NGH=∠ACB
∴tan∠NGH=$\frac{NH}{GN}=\frac{3}{5}$,
∴GN=$\frac{5}{3}NH$=$\frac{11}{3}t-7-\frac{5\sqrt{34}}{3}$,
∴S=S正方形KSMN-S△GNH,
=t2-$\frac{1}{2}$GN•NH,
=t2-$\frac{1}{2}$($\frac{11}{3}t-7-\frac{5\sqrt{34}}{3}$)($\frac{11}{5}t-\frac{21}{5}-\sqrt{34}$),
=-$\frac{91}{30}{t}^{2}+\frac{462+110\sqrt{34}}{30}t-\frac{1291+210\sqrt{34}}{30}$;
③当$\frac{21+5\sqrt{34}}{8}$<t≤7时,如图7,设KS与AC交于G,MN于AC交于H,则正方形KSMN与△ABC重叠部分的面积是梯形GSMH的面积, MC=7+$\frac{5\sqrt{34}}{3}$-2t,MH=$\frac{21}{5}+\sqrt{34}$-$\frac{6}{5}t$,
MC=7+$\frac{5\sqrt{34}}{3}$-2t,MH=$\frac{21}{5}+\sqrt{34}$-$\frac{6}{5}t$,
同理得:SG=$\frac{3}{5}(7+\frac{5\sqrt{34}}{3}-t)$=$\frac{21}{5}+\sqrt{34}-\frac{3}{5}t$,
∴S=S梯形GSMH=$\frac{1}{2}$(MH+SG)•SM=$\frac{1}{2}$($\frac{21}{5}+\sqrt{34}-\frac{6t}{5}+\frac{21}{5}+\sqrt{34}-\frac{3t}{5}$)•t=-$\frac{9}{10t}{t}^{2}+(\frac{21}{5}+\sqrt{34})t$;
综上所述,S与移动的时间t的函数关系式为:
①S=t2(0≤t≤$\frac{21+5\sqrt{34}}{11}$);
②S=-$\frac{91}{30}{t}^{2}+\frac{462+110\sqrt{34}}{30}t-\frac{1291+210\sqrt{34}}{30}$($\frac{21+5\sqrt{34}}{11}<t≤\frac{21+5\sqrt{34}}{8}$);
③S=-$\frac{9}{10}{t}^{2}+(\frac{21}{5}+\sqrt{34})t$($\frac{21+5\sqrt{34}}{8}<t≤7$);
(3)存在.
①当点Q在AC上时,OG=OF=5,如图8,
∵点Q即为点G,
∴△OPQ≌△OPH,
∵F(5,0),直线CE解析式为:y=-$\frac{3}{5}$x+$\sqrt{34}$,
∴P(5,-3+$\sqrt{34}$).
②当P与E重合时,如图9,
∴△POQ≌△POH,
∴Q(-5,0),P(0,$\sqrt{34}$);
综上所述,点P(5,-3+$\sqrt{34}$)或(0,$\sqrt{34}$).
点评 本题是一次函数的综合题,考查了一次函数综合应用,同时题目对面积求解、全等三角形进行考查,题目运算较难,需要注意运算的正确性,在计算重叠部分图形的面积时,利用数形结合的思想,先计算特殊位置时对应的t值,再根据图形特点分类讨论.

| 单价(万元/台) | 每台处理污水量(吨/月) | |
| A型 | 12 | 220 |
| B型 | 10 | 200 |
(2)经预算,市污水处理厂购买设备的资金不超过112万元,月处理污水量不低于2080吨,请你列举出所有购买方案,并指出哪种方案最省钱,需要多少资金?
| A. | 29.848 | B. | 29.749 | C. | 29.806 | D. | 29.795 |
 如图,点A、B、C、D在⊙O上,BC是⊙O的直径,若∠D=36°,则∠BCA的度数是( )
如图,点A、B、C、D在⊙O上,BC是⊙O的直径,若∠D=36°,则∠BCA的度数是( )| A. | 54° | B. | 72° | C. | 45° | D. | 36° |
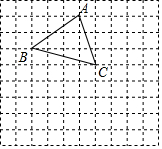 在边长为1的正方形网格中,△ABC的位置如图所示:
在边长为1的正方形网格中,△ABC的位置如图所示: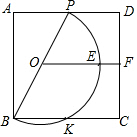 如图,正方形ABCD的边长为4,点P为线段AD上的一动点(不与点A、D重合),以BP为直径作半圆,圆心为点O,半圆O边BC交于点K,线段OF∥AD,且与CD相交于点F,与半圆O相交于点E,设AP=x.
如图,正方形ABCD的边长为4,点P为线段AD上的一动点(不与点A、D重合),以BP为直径作半圆,圆心为点O,半圆O边BC交于点K,线段OF∥AD,且与CD相交于点F,与半圆O相交于点E,设AP=x.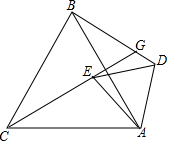 如图,△ABC、△ADE都是等边三角形,点G为射线BD,CE的交点.
如图,△ABC、△ADE都是等边三角形,点G为射线BD,CE的交点.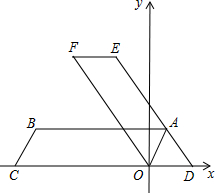 如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将?ABCO绕点O顺时针旋转α°(0<α<90°)得到?DEFO,点A的对应点点D恰好落在x轴的正半轴上,且DE经过点A.
如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将?ABCO绕点O顺时针旋转α°(0<α<90°)得到?DEFO,点A的对应点点D恰好落在x轴的正半轴上,且DE经过点A.