题目内容
14. 北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=3米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=3米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
分析 过C点作AB的垂线交AB的延长线于点D,通过解Rt△ADC得到AD=2CD=2x,在Rt△BDC中利用锐角三角函数的定义即可求出CD的值.
解答 解:作CD⊥AB交AB延长线于D,设CD=x 米.
Rt△ADC中,∠DAC=25°,
所以tan25°=$\frac{CD}{AD}$=0.5,
所以AD=$\frac{CD}{0.5}$=2x.
Rt△BDC中,∠DBC=60°,
由tan 60°=$\frac{2}{2x-3}=\sqrt{3}$,
解得:x≈2.
所以生命迹象所在位置C的深度约为2米.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
9.函数y=$\sqrt{x-2}$+1中,自变量x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤2 |
6.若用代入法解方程组$\left\{\begin{array}{l}{2x=3y}\\{3x=2y+1}\end{array}\right.$,以下各式代入正确的是( )
| A. | 3x=2($\frac{2}{3}$x)+1 | B. | 3x=2($\frac{2}{3}$y)+1 | C. | 3x=2($\frac{3}{2}$x)+1 | D. | 3x=2x•6x+1 |
3. 如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )
如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )
 如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )
如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
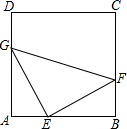 如图,正方形ABCD中,点E,F,G分别为边AB,BC,AD上的点,且AE=BF=DG,连接EF,GE,GF.
如图,正方形ABCD中,点E,F,G分别为边AB,BC,AD上的点,且AE=BF=DG,连接EF,GE,GF.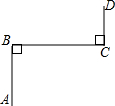 如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是AB∥CD.
如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是AB∥CD.