题目内容
8.小聪是一名非常爱钻研的七年级学生,他将4块完全一样的三角板(如图1)拼成了一个非常工整的图形(如图2),请教老师以后得知:该图形是一个正方形,并且里面的四边形也是一个正方形.为了作进一步的探究,小明将三角板的三边长用为a,b,c表示(如图3),将两个正方形分别用正方形ABCD和正方形EFGH表示,然后他用两种不同的方法计算了正方形ABCD的面积.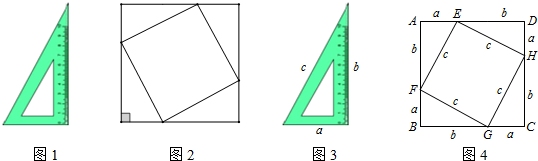
(1)请你用两种不同的方法计算出正方形ABCD面积:
方法一:方法二:
(2)根据(1)中计算结果,你能得到怎么样的结论?
(3)请用文字语言描述(2)中得到的结论.
分析 (1)方法一:直接利用正方形的面积公式计算;方法二:计算4个直角三角形的面积和边长为c的正方形的面积和可得到正方形ABCD的面积;
(2)利用面积相等易得c2=a2+b2;
(3)结论为勾股定理.
解答 解:(1)方法一:正方形ABCD的面积=(a+b)2=a2+2ab+b2;
方法二:正方形ABCD的面积=4•$\frac{1}{2}$ab+c2=c2+2ab,
(2)由(1)得c2=a2+b2;
(3)结论:直角三角形的两直角边的平方和等于斜边的平方.
点评 本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.解决本题的关键是掌握勾股定理的推导.

练习册系列答案
相关题目
16.如果$\frac{6sinα-2cosα}{2sinα+cosα}$=2,那么tanα=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
20.已知点(x1,y1)、(x2,y2)、(x3,y3)在双曲线$y=\frac{5}{x}$上,当x1<0<x2<x3时,y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y3<y1 |
17.已知a,b是一元二次方程x2-2x-1=0的两个实数根,则代数式(a-b)(a+b-2)+ab的值等于( )
| A. | -1 | B. | 1 | C. | ±8$\sqrt{2}$-1 | D. | ±8$\sqrt{2}$+1 |
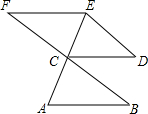 如图,点C既是AE的中点,也是BF为中点,AB∥CD,∠D=∠F,说明BC∥DE的理由.
如图,点C既是AE的中点,也是BF为中点,AB∥CD,∠D=∠F,说明BC∥DE的理由.
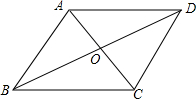 如图所示,在菱形ABCD中,∠BAD=120°,AB=4.
如图所示,在菱形ABCD中,∠BAD=120°,AB=4.