题目内容
3.直线y=-x+m与直线y=x-2的交点在第一象限,求m的取值范围.分析 联立两直线解析式求出交点坐标,再根据交点在第一象限列出不等式组求解即可.
解答 解:根据题意,联立方程组$\left\{\begin{array}{l}{y=-x+m}\\{y=x-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{m+2}{2}}\\{y=\frac{m-2}{2}}\end{array}\right.$,
则两直线交点坐标为($\frac{m+2}{2}$,$\frac{m-2}{2}$),
∵两直线交点在第一象限,
∴$\left\{\begin{array}{l}{\frac{m+2}{2}>0}\\{\frac{m-2}{2}>0}\end{array}\right.$,
解得:m>2.
点评 本题考查了两直线相交的问题,解一元一次不等式组,联立两函数解析式求交点坐标是常用的方法.

练习册系列答案
相关题目
14.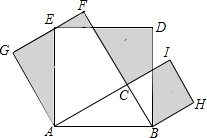 如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )
 如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )| A. | 60 | B. | 90 | C. | 144 | D. | 169 |
18.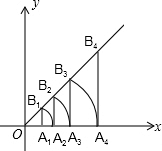 如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )
如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )
 如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )
如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )| A. | ($\sqrt{2}$)n-1 | B. | ($\sqrt{2}$)n | C. | ($\sqrt{2}$)n+1 | D. | 2n |
13.反比例函数y=$\frac{k}{x}$的图象经过点A(-2,-5),则当1<x<2时,y的取值范围是( )
| A. | -10<y<-5 | B. | -2<y<-1 | C. | 5<y<10 | D. | y>10 |
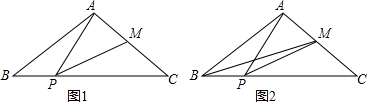 如图,在△ABC中,己知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.
如图,在△ABC中,己知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.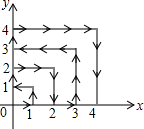 如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(1,0),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(0,1)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(0,5).
如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(1,0),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(0,1)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(0,5).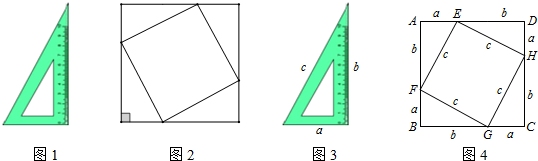
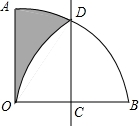 如图,扇形AOB的圆心角为90°,半径为2,点C为OB中点,点D在$\widehat{AB}$上,将扇形沿直线CD折叠,若点B,O重合,则图中阴影部分的周长为π+2.(结果保留π)
如图,扇形AOB的圆心角为90°,半径为2,点C为OB中点,点D在$\widehat{AB}$上,将扇形沿直线CD折叠,若点B,O重合,则图中阴影部分的周长为π+2.(结果保留π)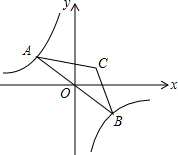 如图,点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为3.
如图,点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为3.