题目内容
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D 在BC上,且CD=3cm,现有两个动点P,Q 分别从点A和点B 同时出发,其中点P以1cm/秒的速度沿AC 向终点C 运动;点Q以1.25cm/秒的速度沿BC 向终点C运动.过点P作PE∥BC交AD于点E,连接PQ,EQ.设动点运动时间为t秒(0<t≤4 ).解答下列问题:
(1)判定直线PQ与直线AB的位置关系,并说明理由;
(2)设△EPQ的面积为y(cm2),求y与t之间的函数关系式;
(3)设线段PQ的长为x(cm),求y与x之间的函数关系式;
(4)是否存在某一时刻t,使△EDQ为直角三角形?若存在,求出此时t的值,若不存在,请说明理由.

(1)判定直线PQ与直线AB的位置关系,并说明理由;
(2)设△EPQ的面积为y(cm2),求y与t之间的函数关系式;
(3)设线段PQ的长为x(cm),求y与x之间的函数关系式;
(4)是否存在某一时刻t,使△EDQ为直角三角形?若存在,求出此时t的值,若不存在,请说明理由.

考点:相似形综合题
专题:
分析:(1)根据已知条件得出
=
,再根据∠C=∠C,得出△PQC∽△ABC,即可得出∠PQC=∠B,从而得出PQ∥AB;
(2)根据已知和AA得出△APE∽△ADC,求出PE的值,即可得出y与t之间的函数关系式;
(3)由(1)得出△PQC∽△ABC,求出PQ=
(4-t)=x,求出t的值,即可得出y与t之间的函数关系式;
(4)由于∠EDQ≠90°,当△EDQ为直角三角形时,可分两种情况进行讨论:∠QED=90°和∠EQP=90°,两种情况都可以通过证明三角形相似,列出比例关系式,从而求出t的值.
| PC |
| AC |
| QC |
| BC |
(2)根据已知和AA得出△APE∽△ADC,求出PE的值,即可得出y与t之间的函数关系式;
(3)由(1)得出△PQC∽△ABC,求出PQ=
| ||
| 4 |
(4)由于∠EDQ≠90°,当△EDQ为直角三角形时,可分两种情况进行讨论:∠QED=90°和∠EQP=90°,两种情况都可以通过证明三角形相似,列出比例关系式,从而求出t的值.
解答:解:(1)直线PQ与直线AB平行;
∵AP=t厘米,BQ=1.25t厘米,AC=4厘米,BC=5厘米,
∴
=
,
=
=
,
∴
=
,
又∵∠C=∠C,
∴△PQC∽△ABC,
∴∠PQC=∠B,
∴PQ∥AB,
∴在运动过程中,不论t 取何值时,总有线段PQ与线段AB平行;
(2)∵PE∥BC,
∴∠AEP=∠ADC,
又∵∠DAC=∠DAC,
∴△APE∽△ADC
∴
=
,
∴PE=
t,
∴y=
PE•PC=
t(4-t);
(3)由(1)得△PQC∽△ABC,
∴
=
,
∴PQ=
(4-t)=x,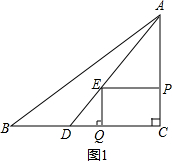
∴4-t=
x
t=4-
x,
∴y=
;
(4)分两种情况讨论:
①如图1:当∠EQD=90°时,显然有EQ=PC=4-t,DQ=1.25t-2,
又∵EQ∥AC,
∴△EDQ∽△ADC,
∴
=
,即
=
,
解得t=2.5;
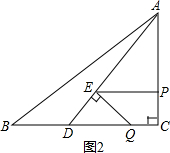
②如图2:当∠QED=90°时,
∵∠CDA=∠EDQ,∠QED=∠C=90°,
∴△EDQ∽△CDA,
∴
=
,
∴Rt△EDQ斜边上的高为4-t,Rt△CDA斜边上的高为2.4,
∴
=
,
解得t=3.1.
综上所述,当t为2.5秒或3.1秒时,△EDQ为直角三角形.
∵AP=t厘米,BQ=1.25t厘米,AC=4厘米,BC=5厘米,
∴
| PC |
| AC |
| 4-t |
| 4 |
| QC |
| BC |
| 5-1.25t |
| 5 |
| 4-t |
| 4 |
∴
| PC |
| AC |
| QC |
| BC |
又∵∠C=∠C,
∴△PQC∽△ABC,
∴∠PQC=∠B,
∴PQ∥AB,
∴在运动过程中,不论t 取何值时,总有线段PQ与线段AB平行;
(2)∵PE∥BC,
∴∠AEP=∠ADC,
又∵∠DAC=∠DAC,
∴△APE∽△ADC
∴
| PE |
| DC |
| AP |
| AC |
∴PE=
| 3 |
| 4 |
∴y=
| 1 |
| 2 |
| 3 |
| 8 |
(3)由(1)得△PQC∽△ABC,
∴
| PQ |
| AB |
| PC |
| AC |
∴PQ=
| ||
| 4 |

∴4-t=
4
| ||
| 41 |
t=4-
4
| ||
| 41 |
∴y=
6
| ||
| 41 |
(4)分两种情况讨论:
①如图1:当∠EQD=90°时,显然有EQ=PC=4-t,DQ=1.25t-2,
又∵EQ∥AC,
∴△EDQ∽△ADC,
∴
| EQ |
| AC |
| DQ |
| DC |
| 4-t |
| 4 |
| 1.25t-2 |
| 3 |

解得t=2.5;
②如图2:当∠QED=90°时,
∵∠CDA=∠EDQ,∠QED=∠C=90°,
∴△EDQ∽△CDA,
∴
| DQ |
| DA |
| Rt△EDQ斜边的高 |
| Rt△CDA斜边的高 |
∴Rt△EDQ斜边上的高为4-t,Rt△CDA斜边上的高为2.4,
∴
| 1.25t-2 |
| 5 |
| 4-t |
| 2.4 |
解得t=3.1.
综上所述,当t为2.5秒或3.1秒时,△EDQ为直角三角形.
点评:此题考查了相似形综合,用到的知识点是平行线的判定、相似三角形的判定与性质、平行四边形及直角三角形的性质等,关键是根据题意画出图形,构造直角三角形,注意分情况讨论,不要漏解.

练习册系列答案
相关题目
 如图,在△AOB中,∠AOB=90°,
如图,在△AOB中,∠AOB=90°, 如图,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.
如图,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线. 如图,四边形AOCD是矩形纸片,点D坐标为(4,3),把矩形沿OD所在直线折叠,点C落在点B处,则重叠部分△POD的面积为
如图,四边形AOCD是矩形纸片,点D坐标为(4,3),把矩形沿OD所在直线折叠,点C落在点B处,则重叠部分△POD的面积为