题目内容
已知:关于mx2-2(m-1)x+m-2=0的一元二次方程(m>0).
(1)求证:方程总有两个不相等的实数根;
(2)m取何整数值时,此方程的两个实数根都为整数?
(1)求证:方程总有两个不相等的实数根;
(2)m取何整数值时,此方程的两个实数根都为整数?
考点:根的判别式
专题:计算题
分析:(1)先计算判别式的值得到△=4,然后根据判别式的意义即可得到方程总有两个不相等的实数根;
(2)利用求根公式法解方程得到x1=1,x2=
=1-
,然后利用有理数的整除性确定m的值.
(2)利用求根公式法解方程得到x1=1,x2=
| m-2 |
| m |
| 2 |
| m |
解答:(1)证明:∵m>0,△=[-2(m-1)]2-4m(m-2)=4m2-8m+4-4m2+8m=4>0,
∴此方程总有两个不等实根;
(2)解:由求根公式得x1=1,x2=
=1-
,
∵方程的两个根均为整数且m是整数,
∴1-
是整数,即
是整数,
而m>0,
∴m=1或2.
∴此方程总有两个不等实根;
(2)解:由求根公式得x1=1,x2=
| m-2 |
| m |
| 2 |
| m |
∵方程的两个根均为整数且m是整数,
∴1-
| 2 |
| m |
| 2 |
| m |
而m>0,
∴m=1或2.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
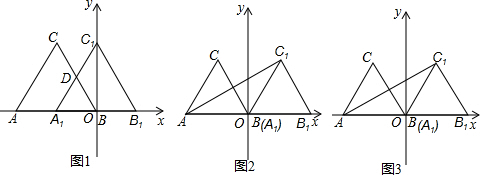
 如图,在平面直角坐标系中,A(6,0),B(6,3),画出所有以原点O为位似中心,将△ABO缩小为原来的
如图,在平面直角坐标系中,A(6,0),B(6,3),画出所有以原点O为位似中心,将△ABO缩小为原来的
 如图,平行四边形ABCD中,点M为BC边中点,且AM=9,BD=12,AD=10,AM与BD的交于点E.求证:AM⊥BD.
如图,平行四边形ABCD中,点M为BC边中点,且AM=9,BD=12,AD=10,AM与BD的交于点E.求证:AM⊥BD. 如图,已知在矩形ABCD中,AD=10,CD=5,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,当B、E、F三点共线时,两点同时停止运动,此时BF⊥CE.设点E移动的时间为t(秒).
如图,已知在矩形ABCD中,AD=10,CD=5,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,当B、E、F三点共线时,两点同时停止运动,此时BF⊥CE.设点E移动的时间为t(秒). 如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=40°,则∠BOC=
如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=40°,则∠BOC=