Question

如图，在△AOB中，∠AOB=90°，

AO

BO

=

3

4

，若⊙O的半径为r=

12

5

，请判断命题“当

3

2

≤S_△ABO≤6时，直线AB一定和⊙O相交”是否正确，如果正确请说明理由，错误请举出反例．

Answer 1

考点：直线与圆的位置关系

专题：

分析：首先根据

AO

BO

=

3

4

，设OA=3k，OB=4k（k＞0），利用勾股定理得到AB=5k，作OH⊥AB于H，利用等积法求得OH，从而求得S_△ABO，根据

3

2

≤S_△ABO≤6时得到直线AB与⊙O相切，从而举出反例，判断命题错误．

解答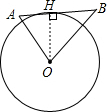：答：不正确．理由如下：
解：∵

AO

BO

=

3

4

，
∴设OA=3k，OB=4k（k＞0），
∵∠AOB=90°，
∴AB=5k
作OH⊥AB于H，则OH=

12k

5

，
S_△ABO=

1

2

OA•OB=

1

2

×3k×4k=6k²，
∵当

3

2

≤S_△ABO≤6时，

3

2

≤6k²≤6，
∴

1

4

≤k²≤1，
设y=k²，
∵k＞0，
∴当y=

1

4

时，k=

1

2

；当y=1时，k=1，
∵当k＞0时，y随着k的增大而增大，
∴

1

2

≤k≤1，
当k=1时，OH=

12

5

=r，
又∵OH⊥AB，
∴直线AB与⊙O相切，
“当

3

2

≤S_△ABO≤6时，直线AB一定和⊙O相交”是不正确的．

点评：本题考查了直线与圆的位置关系，解题的关键是能够举出反例，难度较大，题型比较新颖．