题目内容
2.当m为何值时,分式方程$\frac{2}{x-2}$+$\frac{mx}{{x}^{2}-4}$=0无解?分析 首先解分式方程,进而利用分式方程无解得出x的值,即可得出答案.
解答 解:分式方程$\frac{2}{x-2}$+$\frac{mx}{{x}^{2}-4}$=0
去分母得:2(x+2)+mx=0,
整理得:(2+m)x=-4,
解得:x=$\frac{-4}{2+m}$,
当x=±2时或2+m=0时,分式方程$\frac{2}{x-2}$+$\frac{mx}{{x}^{2}-4}$=0无解,
解得:m=-2或-4或0.
点评 此题主要考查了分式方程的解,正确解分式方程再分类讨论是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如表列出了皮球反弹高度和下落高度的数据,其中d表示皮球的下落高度,h表示皮球落地后的反弹高度(单位:cm)
(1)表中反映了哪两个变量之间的关系?哪个是自变量?哪个是函数?
(2)当下落高度是100cm时,皮球的反弹高度是多少?
(2)预测下落高度是90cm时,皮球的反弹高度是多少?
| d | 50 | 80 | 100 | 150 |
| h | 25 | 40 | 50 | 75 |
(2)当下落高度是100cm时,皮球的反弹高度是多少?
(2)预测下落高度是90cm时,皮球的反弹高度是多少?
10.已知点(-4,y1)(1,y2)都在直线y=$\frac{2}{3}$x-4上,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能比较 |
14.计算:$\frac{4}{{x}^{2}-4}$-$\frac{1}{x-2}$的正确结果是( )
| A. | -$\frac{1}{x+2}$ | B. | 1-x | C. | 1 | D. | -1 |
 -$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$
-$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$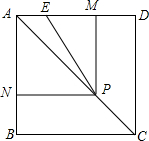 如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.