题目内容
14．计算：$\frac{4}{{x}^{2}-4}$-$\frac{1}{x-2}$的正确结果是（ ）| A． | -$\frac{1}{x+2}$ | B． | 1-x | C． | 1 | D． | -1 |
分析 先将分母因式分解以确定最简公分母为（x+2）（x-2），再通分化为同分母分式相减，最后将分式约分化为最简分式．
解答 解：原式=$\frac{4}{（x+2）（x-2）}$-$\frac{x+2}{（x+2）（x-2）}$
=$\frac{4-x-2}{（x+2）（x-2）}$
=$\frac{-（x-2）}{（x+2）（x-2）}$
=-$\frac{1}{x+2}$，
故选：A．
点评 本题主要考查分式的加减运算，异分母分式相加减，先通分，变为同分母分式，再利用同分母分式的加减法则计算．
练习册系列答案
名校课堂系列答案
相关题目
19．若一次函数y=kx+b的图象经过点P（-2，3），则2k-b的值为（ ）
| A． | 2 | B． | -2 | C． | 3 | D． | -3 |
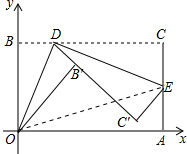如图，将矩形纸片ABCD置于直角坐标系中，点A（4，0），点B（0，3），点D（异于点B、C）为边BC上动点，过点O、D折叠纸片，得点B′和折痕OD．过点D再次折叠纸片，使点C落在直线DB′上，得点C′和折痕DE，连接OE，设BD=t．
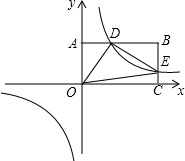如图，反比例函数y=$\frac{k}{x}$（k＞0）与长方形OABC在第一象限相交于D、E两点，OA=2，OC=4，连结OD、OE、DE．记△OAD、△OCE的面积分别为S1、S2．
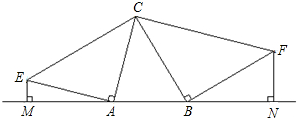如图，锐角△ABC分别以A、B为直角顶点，向△ABC外作等腰直角三角形ACE和等腰直角三角形BCF，再分别过点E、F作边AB所在直线的垂线，垂足为M，N．