题目内容
11.在数学课上,老师提出如下问题:如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.
小明的折叠方法如下:
如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D; (2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.
老师说:“小明的作法正确.”
请回答:小明这样折叠的依据是CD和EF是四边形DECF对角线,而CD和EF互相垂直且平分(答案不唯一).
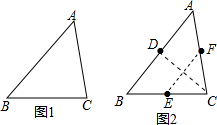
分析 根据折叠的性质得到CD和EF互相垂直且平分,结合菱形的判定定理“对角线互相垂直平分的四边形是菱形”证得结论.
解答  解:如图,连接DF、DE.
解:如图,连接DF、DE.
根据折叠的性质知,CD⊥EF,且OD=OC,OE=OF.
则四边形DECF恰为菱形.
故答案是:CD和EF是四边形DECF对角线,而CD和EF互相垂直且平分(答案不唯一).
点评 本题考查了菱形的判定,翻折变换(折叠问题).
总结:①菱形定义:一组邻边相等的平行四边形是菱形(平行四边形+一组邻边相等=菱形);
②四条边都相等的四边形是菱形.
③对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱形”).

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
19.若一次函数y=kx+b的图象经过点P(-2,3),则2k-b的值为( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
16.九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如表:
已知该运动服的进价为每件60元,设售价为x元.销量该运动服每件的利润为y元,销量为W件,其中W与x成一次函数关系.
(1)写出y与x的函数关系式;
(2)求出W与x的函数关系式;
(3)售价为150元时,月销售量是多少?
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
(1)写出y与x的函数关系式;
(2)求出W与x的函数关系式;
(3)售价为150元时,月销售量是多少?
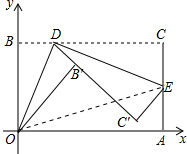 如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.
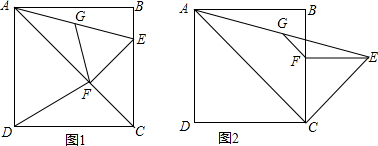
如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.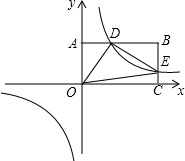 如图,反比例函数y=$\frac{k}{x}$(k>0)与长方形OABC在第一象限相交于D、E两点,OA=2,OC=4,连结OD、OE、DE.记△OAD、△OCE的面积分别为S1、S2.
如图,反比例函数y=$\frac{k}{x}$(k>0)与长方形OABC在第一象限相交于D、E两点,OA=2,OC=4,连结OD、OE、DE.记△OAD、△OCE的面积分别为S1、S2.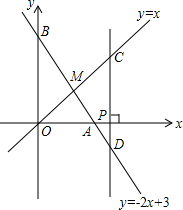 如图,已知函数y=-2x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.在X轴上有一点P(a,0)(其中a>1),过点P作x轴的垂线,分别交函数y=x和y=-2x+3的图象于点C、D.若CD=3,求a的值.
如图,已知函数y=-2x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.在X轴上有一点P(a,0)(其中a>1),过点P作x轴的垂线,分别交函数y=x和y=-2x+3的图象于点C、D.若CD=3,求a的值.