题目内容
5.若直角三角形的两直角边为a、b且满足$\sqrt{9-6a+{a}^{2}}$+|b-4|=0,则该直角三角形的斜边长为5.分析 利用非负数的性质得出a,b的值,进而利用勾股定理得出斜边长.
解答 解:∵$\sqrt{9-6a+{a}^{2}}$+|b-4|=0,
∴$\sqrt{(a-3)^{2}}$+|b-4|=0,
∴a-3=0,b-4=0,
∴a=3,b=4,
∴该直角三角形的斜边长为:5.
故答案为:5.
点评 此题主要考查了勾股定理以及非负数的性质,得出a,b的值是解题关键.

练习册系列答案
相关题目
20.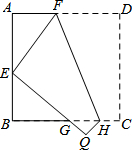 如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是( )
如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是( )
 如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是( )
如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
 如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=α,DE交AC于点E.下列结论:
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=α,DE交AC于点E.下列结论: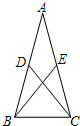 如图,△ABC中,AB=AC,点D、E分别是AB、AC的中点.求证:BE=CD.
如图,△ABC中,AB=AC,点D、E分别是AB、AC的中点.求证:BE=CD.