题目内容
6.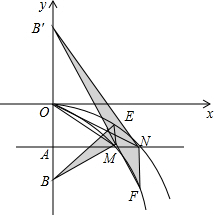 如图,在平面直角坐标系中,点A(0,-a2)(a>0)在y轴的负半轴上,过点A作x轴的平行线,分别交抛物线C1:y=-$\frac{1}{2}$x2(x>0)于点M,交抛物线C2:y=-$\frac{1}{4}{x}^{2}$(x>0)于点N,连接OM,ON.
如图,在平面直角坐标系中,点A(0,-a2)(a>0)在y轴的负半轴上,过点A作x轴的平行线,分别交抛物线C1:y=-$\frac{1}{2}$x2(x>0)于点M,交抛物线C2:y=-$\frac{1}{4}{x}^{2}$(x>0)于点N,连接OM,ON.(1)填空:当a=1时,$\frac{AM}{AN}$=$\frac{\sqrt{2}}{2}$;当a=2时,$\frac{AM}{AN}$=$\frac{\sqrt{2}}{2}$;当a=3时,$\frac{AM}{AN}$=$\frac{\sqrt{2}}{2}$;由上可猜想:对于任意正数a,都有$\frac{AM}{AN}$=$\frac{\sqrt{2}}{2}$;证明你的猜想;
(2)当△OAM和△OAN中有一个是等腰三角形时,S△OAN-S△OAM的值;
(3)过点M作y轴平行线交抛物线C2于点E,过点N作y轴的平行线交抛物线C1于点F,在y轴上任取一组关于点O对称的点B,B′,连接BE,BM,B′F,B′N,求S△BDA与S△MFN的比值.
分析 (1)当a=1时点A坐标是(0,-1),分别求出-$\frac{1}{2}$x2=-1、-$\frac{1}{4}{x}^{2}$=-1时x的值,可得AM、AN的长度,继而可得$\frac{AM}{AN}$,当a=2、a=3及任意正数a时,相同作法可得;
(2)△OAM和△OAN中有一个是等腰三角形有两种可能:①当△OAM为等腰三角形时,AM=OA=-a2,②当△OAN为等腰三角形时,AN=OA,分别求出每种情况下△OAM和△OAN的面积即可;
(3)由M、N两点的纵坐标-a2表示出ME、NF的长及两点到y轴距离,进而可得△BDA、△MFN的面积表达式,即可知S△BDA与S△MFN的比值.
解答 解:(1)当a=1时,点A坐标为(0,-1),
由-$\frac{1}{2}$x2=-1得x=$±\sqrt{2}$,即AM=$\sqrt{2}$,
由-$\frac{1}{4}{x}^{2}$=-1得x=±2,即AN=2,则$\frac{AM}{AN}$=$\frac{\sqrt{2}}{2}$;
当a=2时,点A坐标为(0,-4),
由-$\frac{1}{2}$x2=-4得x=$±2\sqrt{2}$,即AM=2$\sqrt{2}$,
由-$\frac{1}{4}{x}^{2}$=-4得x=±4,即AN=4,则$\frac{AM}{AN}$=$\frac{\sqrt{2}}{2}$;
当a=3时,点A的坐标为(0,-9),
由-$\frac{1}{2}$x2=-9得x=$±3\sqrt{2}$,即AM=3$\sqrt{2}$,
由-$\frac{1}{4}{x}^{2}$=-9得x=±6,即AN=6,则$\frac{AM}{AN}$=$\frac{\sqrt{2}}{2}$;
对于任意正数a,都有$\frac{AM}{AN}$=$\frac{\sqrt{2}}{2}$,
证明:当y=-a2时,由-$\frac{1}{2}$x2=-a2(x>0),解得x=$\sqrt{2}$a,
由-$\frac{1}{4}$x2=-a2(x>0),解得x=2a,
∴AM=$\sqrt{2}$a,AN=2a,
∴$\frac{AM}{AN}$=$\frac{\sqrt{2}}{2}$;
(2)显然∠OAM=∠OAN=90°.
①当△OAM为等腰三角形时,AM=OA=-a2,
∴-$\frac{1}{2}$a4=-a2(a>0),解得a=$\sqrt{2}$,此时x=2,
∴S△OAM=2.
当a=$\sqrt{2}$时,-$\frac{1}{4}$x2=-2,解得x=2$\sqrt{2}$,
∴S△OAN=2$\sqrt{2}$,
∴S△OAN-S△OAM=2$\sqrt{2}$-2.
②当△OAN为等腰三角形时,AN=OA,
∴-$\frac{1}{4}$a4=-a2(a>0),解得a=2,此时x=4,
∴S△OAN=8.
当a=2时,-$\frac{1}{2}$x2=-4,解得x=2$\sqrt{2}$,
∴S△AOM=4$\sqrt{2}$,
∴S△OAN-S△OAM=8-4$\sqrt{2}$.
(3)由-$\frac{1}{2}$x2=-a2(x>0),解得x=$\sqrt{2}$a.
当x=$\sqrt{2}$a时,y=-$\frac{1}{4}$x2=-$\frac{1}{2}$a2,
∴EM=$\frac{1}{2}$a2,
∴S△BEM=$\frac{\sqrt{2}}{4}$a3.
由-$\frac{1}{4}$x2=-a2(x>0),解得x=2a.
当x=2a时,y=-$\frac{1}{2}$x2=2a2,
∴NF=a2,
S△B′NF=a3,
∴$\frac{{S}_{△BEM}}{{S}_{△B'FN}}$=$\frac{\frac{\sqrt{2}}{4}{a}^{3}}{{a}^{3}}$=$\frac{\sqrt{2}}{4}$
∴S△BEM与S△B′FN的比值为$\frac{\sqrt{2}}{4}$.
故答案为:(1)$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$.
点评 本题主要考查二次函数的综合应用能力及三角形的面积,根据点A的坐标结合函数表达式表示出计算所需线段的长度是解题的关键.

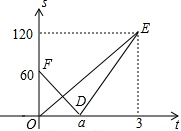 甲、乙两辆遥控车沿直线AC作同方向的匀速运动,甲、乙同时分别从A、B出发,沿轨道到达C处,已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处距离分别为S1,S2,函数关系如图所示,当两车的距离小于10米时,信号会产生相互干扰,那么t是下列哪个值时两车的信号会相互干扰( )
甲、乙两辆遥控车沿直线AC作同方向的匀速运动,甲、乙同时分别从A、B出发,沿轨道到达C处,已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处距离分别为S1,S2,函数关系如图所示,当两车的距离小于10米时,信号会产生相互干扰,那么t是下列哪个值时两车的信号会相互干扰( )| A. | $\frac{2}{3}$ | B. | 2 | C. | $\frac{11}{5}$ | D. | $\frac{13}{5}$ |
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{a}+1$ | C. | a+1 | D. | $\sqrt{a+1}$ |

| A. | 75° | B. | 65° | C. | 60° | D. | 55° |
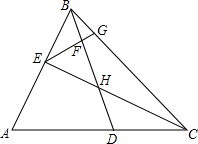 如图,△ABC中,∠A=60°,在AC上截取AD=AB,E为AB上一点,且BE=CD,过点E作BD的垂线,分别交BD、BC于F、G,连接EC交BD于H.
如图,△ABC中,∠A=60°,在AC上截取AD=AB,E为AB上一点,且BE=CD,过点E作BD的垂线,分别交BD、BC于F、G,连接EC交BD于H. 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C'顺时针旋转90°,得到△A″B″C′,
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C'顺时针旋转90°,得到△A″B″C′, 如图,在矩形ABCD中,对角线AC、BD交于点O,若∠AOD=120°,AB=1,则矩形ABCD的面积=$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC、BD交于点O,若∠AOD=120°,AB=1,则矩形ABCD的面积=$\sqrt{3}$.