题目内容
3.如图,△ABC中,AB=AC,点D是任意一点,∠BDA+∠ABC=180°(1)如图1,求证:∠BCA=∠CDA;
(2)如图2,当点D是AC边垂直平分线上的点时,若BD=4,AC=6$\sqrt{7}$,求点D到AC所在直线的距离.
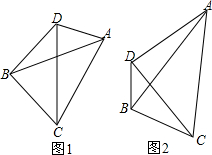
分析 (1)如图1中,只要证明A、C、B、D四点共圆即可.
(2)如图2中,作DE⊥AC于E,AM⊥BD于M、AN⊥CD于N,设DM=DN=x,AM=AN=y,列出方程组解决问题.
解答 解:(1)如图1中,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ADB+∠ABC=180°,
∴∠ADB+∠ACB=180°,
∴A、C、B、D四点共圆,
∴∠ADC=∠ABC=∠ACB.
(2)如图2中,作DE⊥AC于E,AM⊥BD于M、AN⊥CD于N,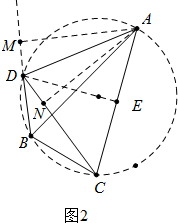
∵A、C、B、D四点共圆,
∴∠ADM=∠ACB=∠ADM,
∴AM=AN,
在△AMD和△AND中,
$\left\{\begin{array}{l}{AD=AD}\\{AM=AN}\end{array}\right.$,
∴△AMD≌△AND,
∴DM=DN,设DM=DN=x,AM=AN=y,
在△ACN和△ABM中,
$\left\{\begin{array}{l}{AC=AB}\\{AN=AM}\end{array}\right.$,
∴△ACN≌△ABM,
∴CN=BM,
∴$\left\{\begin{array}{l}{(x+4)^{2}+{y}^{2}=(6\sqrt{7})^{2}}\\{{x}^{2}+{y}^{2}=(x+x+4)^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=5}\\{y=3\sqrt{19}}\end{array}\right.$,(x<O,y<O已经舍弃).
∵$\frac{1}{2}$•AC•DE=$\frac{1}{2}$•DC•AN,
∴DE=$\frac{DC•AN}{AC}$=$\frac{14×3\sqrt{19}}{6\sqrt{7}}$=$\sqrt{133}$.
点评 本题考查全等三角形的判定和性质、线段垂直平分线的性质、勾股定理,解题的关键是利用方程组解决问题,根据角平分线的性质定理添加辅助线,构造全等三角形,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案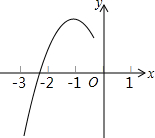 已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac>0;②c-a=3;③a+b+c<0;④方程ax2+bx+c=m(m≥2)一定有实数根,其中正确的结论为( )
| A. | ②③ | B. | ①③ | C. | ①②③ | D. | ①②④ |
| 进价(元/千克) | 售价(元/千克) | |
| 苹果 | 5 | 8 |
| 丑桔 | 9 | 13 |
(2)若该水果店决定丑桔的进货量不超过苹果进货量的3倍,应怎样安排进货才能使水果店在销售完这批水果时获利最多?
 下图中的几何体的左视图是( )
下图中的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,欲得到AF∥CD,可根据( )
如图,欲得到AF∥CD,可根据( )| A. | ∠1=∠2 | B. | ∠6=∠5 | C. | ∠1=∠5 | D. | ∠1=∠3 |
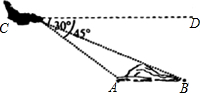 钓鱼岛及周边岛屿自古以来就是中国的领土.如图,我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A、B的俯角∠DCA=45°、∠DCB=30°(己知A、B、C三点在同一平面上),求钓鱼岛南北两端A、B的距离.(参考数据:$\sqrt{3}$=1.73)
钓鱼岛及周边岛屿自古以来就是中国的领土.如图,我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A、B的俯角∠DCA=45°、∠DCB=30°(己知A、B、C三点在同一平面上),求钓鱼岛南北两端A、B的距离.(参考数据:$\sqrt{3}$=1.73)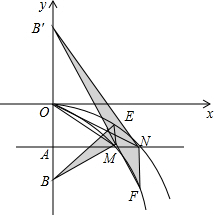 如图,在平面直角坐标系中,点A(0,-a2)(a>0)在y轴的负半轴上,过点A作x轴的平行线,分别交抛物线C1:y=-$\frac{1}{2}$x2(x>0)于点M,交抛物线C2:y=-$\frac{1}{4}{x}^{2}$(x>0)于点N,连接OM,ON.
如图,在平面直角坐标系中,点A(0,-a2)(a>0)在y轴的负半轴上,过点A作x轴的平行线,分别交抛物线C1:y=-$\frac{1}{2}$x2(x>0)于点M,交抛物线C2:y=-$\frac{1}{4}{x}^{2}$(x>0)于点N,连接OM,ON.