题目内容
11. 如图所示,已知△ABC中,∠ABC=45°,高AD和BE相交于点F,若BC=11,CD=4,则线段AF的长度是( )
如图所示,已知△ABC中,∠ABC=45°,高AD和BE相交于点F,若BC=11,CD=4,则线段AF的长度是( )| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
分析 求出△DBF≌△DAC,根据全等三角形的性质得出DF=DC,求出AD=BD=7,即可求出答案.
解答 解:∵高AD和BE相交于点F,
∴∠ADC=∠BDF=90°,∠BEC=90°,
∵∠DBF+∠C+∠BEC=180°,∠C+∠DAC+∠ADC=180°,
∴∠DBF=∠DAC,
∵∠ADB=90°,∠ABC=45°,
∴∠BAD=180°-90°-45°=45°=∠ABD,
∴AD=BD,
在△DBF和△DAC中
$\left\{\begin{array}{l}{∠DBF=∠DAC}\\{BD=AD}\\{∠FDB=∠ADC}\end{array}\right.$
∴△DBF≌△DAC,
∴DF=DC,
∵BC=11,CD=4,
∴BD=BC-CD=7,DF=4,
∵AD=BD,
∴AD=7,
∴AF=AD-CD=7-4=3,
故选A.
点评 本题考查了全等三角形的性质和判定,能求出△DBF≌△DAC是解此题的关键.

练习册系列答案
相关题目
2.铁一课间餐种类繁多,深受学生喜爱.这天饭堂在课间的出品有鸡腿、薯饼、鱼丸和鸡柳.某同学就九年级学生对课间餐各类食物的喜爱程度做了抽样调查,制成表格如下:
(1)样本容量是250,a=12%,b=30,c=16%.
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.
| 课间餐种类 | 人类 | 百分比 |
| 鸡腿 | 150 | 60% |
| 薯饼 | 30 | a |
| 鱼丸 | b | 12% |
| 鸡柳 | 40 | c |
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.
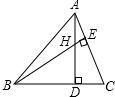 如图,在△ABC中,H是高AD和BE的交点,AD=BD,求证:DH=DC.
如图,在△ABC中,H是高AD和BE的交点,AD=BD,求证:DH=DC.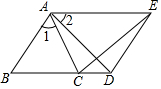 如图,已知∠1=∠2,AB=AC,AD=AE,且B、C、D三点共线.
如图,已知∠1=∠2,AB=AC,AD=AE,且B、C、D三点共线. 如图,AC=AD,BC=BD,图中有相等的角吗?若没有说明理由,若有请全部找出来,并证明其中的一组角相等.
如图,AC=AD,BC=BD,图中有相等的角吗?若没有说明理由,若有请全部找出来,并证明其中的一组角相等.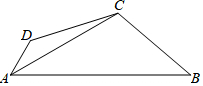 如图,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,AC=4,CD=3,则AB-AD=2$\sqrt{5}$.
如图,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,AC=4,CD=3,则AB-AD=2$\sqrt{5}$. 如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC的三个顶点A(-4,4),B(0,6),C(0,2).
如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC的三个顶点A(-4,4),B(0,6),C(0,2). 已知,如图,∠1=∠2,AB=AE,∠ACB=2∠B.求证:
已知,如图,∠1=∠2,AB=AE,∠ACB=2∠B.求证: