题目内容
19.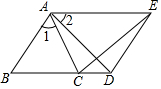 如图,已知∠1=∠2,AB=AC,AD=AE,且B、C、D三点共线.
如图,已知∠1=∠2,AB=AC,AD=AE,且B、C、D三点共线.(1)求证:BD=CE;
(2)求证:AC平分∠BCE;
(3)若∠ADE=70°,求∠ECD的度数.
分析 (1)欲证明BD=EC,只要证明△BAD≌△CAE即可;
(2)由△BAD≌△CAE,可得∠B=∠ACE,由AB=AC,可得∠B=∠ACB即可推出∠ACB=∠ACE;
(3)利用“8字型”证明∠ECD=∠2即可;
解答 (1)证明:∵∠1=∠2,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE,
∴BD=EC.
(2)证明:∵△BAD≌△CAE,
∴∠B=∠ACE,
∵AB=AC,
∴∠B=∠ACB,
∴∠ACB=∠ACE,
∴AC平分∠BCE.
(3)解:设AD交EC于O.
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠2=40°,
∵△BAD≌△CAE,
∴∠ADB=∠AEO,
∵∠AOF=∠COD,
∴∠ECD=∠2=40°
点评 本题考查全等三角形的判定和性质、角平分线的定义、等腰三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,学会利用:“8字型”证明角相等,属于中考常考题型.

练习册系列答案
相关题目
8.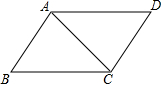 如图,已知AB=CD,AD=CB,则在下列结论中,错误的是( )
如图,已知AB=CD,AD=CB,则在下列结论中,错误的是( )
 如图,已知AB=CD,AD=CB,则在下列结论中,错误的是( )
如图,已知AB=CD,AD=CB,则在下列结论中,错误的是( )| A. | AB∥DC | B. | ∠B=∠D | C. | ∠BAD=∠DCB | D. | AB=AD |
 如图,在四边形ABCD中,AB=CD,AD=BC,点O为BD上任意一点,过点O的直线分别交AD,BC于M,N两点.求证:∠1=∠2.
如图,在四边形ABCD中,AB=CD,AD=BC,点O为BD上任意一点,过点O的直线分别交AD,BC于M,N两点.求证:∠1=∠2.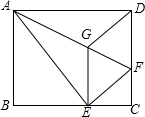 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.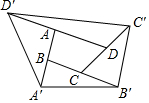 如图,把四边形ABCD的各边延长,使得AB=BA',BC=CB',CD=DC',DA=AD',得到一个大的四边形A'B'C'D',若四边形ABCD的面积是1,求四边形A'B'C'D'的面积.
如图,把四边形ABCD的各边延长,使得AB=BA',BC=CB',CD=DC',DA=AD',得到一个大的四边形A'B'C'D',若四边形ABCD的面积是1,求四边形A'B'C'D'的面积.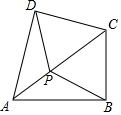 如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,P为对角线AC上任一点,求证:PB=PD.
如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,P为对角线AC上任一点,求证:PB=PD. 如图所示,已知△ABC中,∠ABC=45°,高AD和BE相交于点F,若BC=11,CD=4,则线段AF的长度是( )
如图所示,已知△ABC中,∠ABC=45°,高AD和BE相交于点F,若BC=11,CD=4,则线段AF的长度是( )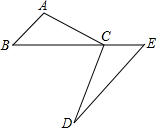 如图,C为BE上一点,点A、D分别在BE两侧,AB∥ED,AB=CE,请你添加一个条件,使△ABC≌△CED,你添加的条件是BC=ED,,并写出证明过程.
如图,C为BE上一点,点A、D分别在BE两侧,AB∥ED,AB=CE,请你添加一个条件,使△ABC≌△CED,你添加的条件是BC=ED,,并写出证明过程.