题目内容
1. 已知,如图,∠1=∠2,AB=AE,∠ACB=2∠B.求证:
已知,如图,∠1=∠2,AB=AE,∠ACB=2∠B.求证:(1)BD=ED;
(2)CD=CE.
分析 (1)根据全等三角形的判定与性质即可得到结论;
(2)根据全等三角形的性质得到∠B=∠E,得到∠ACB=2∠E,于是得到结论.
解答 解:(1)在△ABD与△AED中,$\left\{\begin{array}{l}{AB=AE}\\{∠1=∠2}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△AED,
∴BD=ED;
(2)∵△ABD≌△AED,
∴∠B=∠E,
∴∠ACB=2∠E,
∵∠ACB=∠E+∠CDE,
∴∠E=∠CDE,
∴CD=CE.
点评 本题考查了全等三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
10.若m2+m-1=0,则m3+2m2+2017的值为( )
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
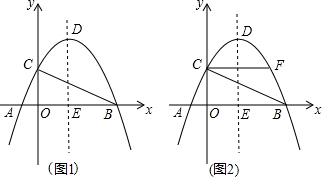
 如图所示,已知△ABC中,∠ABC=45°,高AD和BE相交于点F,若BC=11,CD=4,则线段AF的长度是( )
如图所示,已知△ABC中,∠ABC=45°,高AD和BE相交于点F,若BC=11,CD=4,则线段AF的长度是( ) 如图,已知△ABC,求作△ACD,使得D在边AB上,且△ACD∽△ABC(不写作法,但要保留作图痕迹).
如图,已知△ABC,求作△ACD,使得D在边AB上,且△ACD∽△ABC(不写作法,但要保留作图痕迹).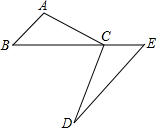 如图,C为BE上一点,点A、D分别在BE两侧,AB∥ED,AB=CE,请你添加一个条件,使△ABC≌△CED,你添加的条件是BC=ED,,并写出证明过程.
如图,C为BE上一点,点A、D分别在BE两侧,AB∥ED,AB=CE,请你添加一个条件,使△ABC≌△CED,你添加的条件是BC=ED,,并写出证明过程.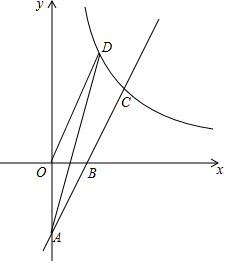 如图,在平面直角坐标系中,直线y=kx-4(k≠0)与坐标轴交于A、B两点,与反比例函数y=$\frac{m}{x}$(m≠0,x>0)在第一象限内的图象交于点C(4,a),反比例函数图象上有一点D(b,6),连接OD和AD,已知:tan∠OAB=$\frac{1}{2}$.
如图,在平面直角坐标系中,直线y=kx-4(k≠0)与坐标轴交于A、B两点,与反比例函数y=$\frac{m}{x}$(m≠0,x>0)在第一象限内的图象交于点C(4,a),反比例函数图象上有一点D(b,6),连接OD和AD,已知:tan∠OAB=$\frac{1}{2}$.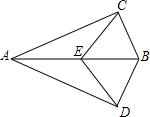 如图,已知:∠ACB和∠ADB都是直角,BC=BD,E是AB上任一点,求证:CE=DE.
如图,已知:∠ACB和∠ADB都是直角,BC=BD,E是AB上任一点,求证:CE=DE.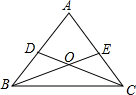 在一次数学课上,周老师在屏幕上出示了一个例题,在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列三个条件:①∠DBO=∠ECO;②BD=CE;③OB=OC.要求同学从这三个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
在一次数学课上,周老师在屏幕上出示了一个例题,在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列三个条件:①∠DBO=∠ECO;②BD=CE;③OB=OC.要求同学从这三个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.