题目内容
7.在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE.(1)如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE=90°°.
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由.
②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出你的结论.

分析 (1)先用等式的性质得出∠CAE=∠BAD,进而得出△ABD≌△ACE,有∠B=∠ACE,最后用等式的性质即可得出结论;
(2)①由(1)的结论即可得出α+β=180°;
②同(1)的方法即可得出结论.
解答 解:(1)∵∠DAE=∠BAC,∠BAC=∠BAD+∠DAC=∠EAC+∠DAC;
∴∠CAE=∠BAD;
在△ABD和△ACE中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△ABD≌△ACE(SAS);
∴∠B=∠ACE;
∴∠BCE=∠BCA+∠ACE=∠BCA+∠B=180°-∠BAC=90°;
故答案为90°;
(2)①由(1)中可知β=180°-α,
∴α、β存在的数量关系为α+β=180°;
②当点D在射线BC上时,如图1,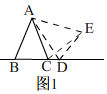
同(1)的方法即可得出,△ABD≌△ACE(SAS);
∴∠ABD=∠ACE,
∴β=∠BCE=∠ACB+∠ACE=∠ACB+∠ABD=180°-∠BAC=180°-α,
∴α+β=180°;
当点D在射线BC的反向延长线上时,如图2,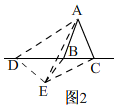
同(1)的方法即可得出,△ABD≌△ACE(SAS);
∴∠ABD=∠ACE,
∴β=∠BCE=∠ACE-∠ACB=∠ABD-∠ACB=∠BAC=α,
∴α=β.
点评 此题是作图---复杂作图,主要考查了等式的性质,全等三角形的判定,解本题的关键是得出△ABD≌△ACE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列各式:$\frac{a-b}{2}$,$\frac{x+3}{x}$,$\frac{5+y}{π}$,$\frac{3}{4}$(x2+1),$\frac{a+b}{a-b}$,$\frac{1}{m}$(a-y)中,是分式的共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.若函数y=(k+1)x2+x+k2+3k-2的图象与y轴交点的纵坐标为-4,则k的值是( )
| A. | -1 | B. | -2 | C. | -1或2 | D. | -1或-2 |
 如图.在△ABC中,∠C=90°,AB的垂直平分线交BC于点M,交AB于点N,若AC=4,CM=3,求S△ABC.
如图.在△ABC中,∠C=90°,AB的垂直平分线交BC于点M,交AB于点N,若AC=4,CM=3,求S△ABC. 小颖利用计算机画出了函数y=x3-3x2-x+4的图象(如图),根据图象,你能求得方程x3-3x2-x+4=0的近似根吗?请写出你的结果,并说出你的理由(结果保留小数点后一位)
小颖利用计算机画出了函数y=x3-3x2-x+4的图象(如图),根据图象,你能求得方程x3-3x2-x+4=0的近似根吗?请写出你的结果,并说出你的理由(结果保留小数点后一位)