题目内容
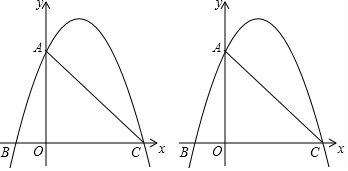
16.如图,在平面直角坐标系中,抛物线y=ax2-bx-3a交x轴于B、C两点,交y轴正半轴于点A,直线y=-x+3经过A、C两点.点P是射线CA上一动点.(1)求抛物线的解析式;
(2)当点P在线段CA上时,P点的横坐标为t,过点P向x轴做垂线交第一象限抛物线于点Q,交x轴于点H,设线段PQ的长为d,求d与t之间的函数关系式;
(3)当点P在线段CA延长线上时,连接BP,取BP中点M,连接MA并延长交抛物线于点R,当AM=AR时,求R点的坐标.
分析 (1)先确定出点A,C的坐标,再用待定系数法求出抛物线解析式;
(2)先表示出点P的坐标,再表示出点Q坐标,即可得出函数关系式;
(3)设出点P坐标,利用中点坐标得出点M坐标,进而求出点R坐标,代入抛物线解析式即可求出t,得出R坐标.
解答 解:(1)∵直线y=-x+3经过A、C两点,
∴A(0,3),C(3,0),
∵抛物线y=ax2-bx-3a交x轴于B、C两点,交y轴正半轴于点A,
∴$\left\{\begin{array}{l}{-3a=3}\\{9a-3b-3a=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴抛物线的解析式y=-x2+2x+3,
(2)如图1,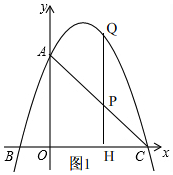
∵点P在线段CA上时,P点的横坐标为t,
∴P(t,-t+3),(0<t<3)
∵过点P向x轴做垂线交第一象限抛物线于点Q,
∴Q(t,-t2+2t+3),
∴d=PQ=-t2+2t+3-(-t+3)=-t2+3t,
(3)如图2,
∵P(t,-t+3),(t>3),B(-1,0),
而M是PB中点,
∴M($\frac{t-1}{2}$,$\frac{-t+3}{2}$),
∵AM=AR,
∴R($\frac{1-t}{2}$,$\frac{t+9}{2}$),
∵点R在抛物线y=-x2+2x+3上,
∴-($\frac{1-t}{2}$)2+2($\frac{1-t}{2}$)+3=$\frac{t+9}{2}$
∴t=-1或t=-3
∴R(1,4)或(2,3).
点评 此题是二次函数综合题,主要考查了待定系数法求抛物线解析式,中点坐标,解本题的过点是确定出抛物线解析式.

练习册系列答案
相关题目
4.填表.
| 单项式 | a | -x2y | -$\frac{5x{y}^{2}z}{2}$ | πx2y | -23a2b3 |
| 系数 | 1 | -1 | -$\frac{5}{2}$ | π | -8 |
| 次数 | 1 | 3 | 4 | 3 | 5 |
5.已知△ABC的周长是24,M是AB的中点,MC=MA=5,则△ABC的面积是( )
| A. | 24 | B. | 20 | C. | 15 | D. | 不确定 |



 如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,BC=8.求△AEG周长.
如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,BC=8.求△AEG周长. 如图,直线l经过第二、三、四象限,l的解析式是y=(m-2)x+n,则m的取值范围在数轴上表示为( )
如图,直线l经过第二、三、四象限,l的解析式是y=(m-2)x+n,则m的取值范围在数轴上表示为( )


