题目内容
2.在△ABC中,∠C=90°,若sinA=$\frac{2}{3}$且AB=4,则AC=3.分析 根据锐角的正弦为对边比斜边,可得BC的长,根据勾股定理,可得AC的长.
解答 解:由在△ABC中,∠C=90°,若sinA=$\frac{2}{3}$且AB=4,得
BC=AB×$\frac{2}{3}$=4×$\frac{2}{3}$=$\frac{8}{3}$,
由勾股定理,得
AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{4}^{2}-(\frac{8}{3})^{2}}$=3,
故答案为:3.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
10.在Rt△ABC中,∠C=90°,若各边都扩大了2倍,则tanA的数值( )
| A. | 没有变化 | B. | 扩大了2倍 | C. | 缩小到$\frac{1}{2}$ | D. | 不能确定 |
 如图,∠MCF=∠FCD,∠MCE=∠ECB,EF=10cm,则CE2+CF2=100cm2.
如图,∠MCF=∠FCD,∠MCE=∠ECB,EF=10cm,则CE2+CF2=100cm2.
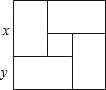 用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则矩形的长为7,宽为5.
用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则矩形的长为7,宽为5. 已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BD为8米,小明将
已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BD为8米,小明将 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,若AB=8,则BD=2.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,若AB=8,则BD=2.