题目内容
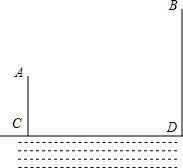
11. 已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BD为8米,小明将
已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BD为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外,将木
梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为7.5m.
分析 先利用等角的余角相等得到∠BAE=∠CED,则可判断Rt△ABE∽△EDC,然后利用相似比计算CD的高度.
解答 解: 如图,BE=3m,DE=BD-BE=8m-3m=5m,
如图,BE=3m,DE=BD-BE=8m-3m=5m,
∵∠AEC=90°,
∴∠AEB+∠CED=90°,
∵∠AEB+∠BAE=90°,
∴∠BAE=∠CED,
∴Rt△ABE∽△EDC,
∴$\frac{BE}{CD}$=$\frac{AB}{DE}$,即$\frac{3}{CD}$=$\frac{2}{5}$,
∴CD=7.5(m).
故答案为7.5m.
点评 本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
3.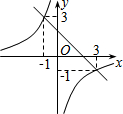 已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
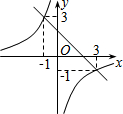 已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )| A. | x<-1或0<x<3 | B. | -1<x<0或x>3 | C. | -1<x<0 | D. | x>3 |
 如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1km,BD=3km,其中CD=3km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小?
如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1km,BD=3km,其中CD=3km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小? 如图,是小明在镜中看到身后墙上的时钟,此时的实际时刻是11:20.
如图,是小明在镜中看到身后墙上的时钟,此时的实际时刻是11:20.