题目内容
12．
如图，∠MCF=∠FCD，∠MCE=∠ECB，EF=10cm，则CE2+CF2=100cm2．
分析 由已知条件得出∠ECF=90°，由勾股定理得出CE2+CF2=EF2，即可得出结果．
解答 解：∵∠MCF=∠FCD，∠MCE=∠ECB，∠MCF+∠FCD+∠MCE+∠ECB=180°，
∴∠MCF+∠MCE=90°，
即∠ECF=90°，
由勾股定理得：CE2+CF2=EF2=102=100（cm2）；
故答案为：100cm2．
点评 本题考查了勾股定理、平角的定义、直角三角形的判定；熟练掌握勾股定理，并能进行推理计算是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．
在如图所示的象棋盘上，建立适当的平面直角坐标系，使“炮”位于点（-1，1）上，“相”位于点（4，-2）上，则“帅”位于点（ ）
在如图所示的象棋盘上，建立适当的平面直角坐标系，使“炮”位于点（-1，1）上，“相”位于点（4，-2）上，则“帅”位于点（ ）| A． | （-3，3） | B． | （-2，2） | C． | （3，-3） | D． | （2，-1） |
如图，以⊙O的直径BC为边作等边△ABC，AB，AC分别交⊙O于点D，E．求证：BD=DE=EC．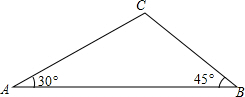
如图，在△ABC中，∠A=30°，∠B=45°，AB=12+12$\sqrt{3}$，求△ABC的面积．
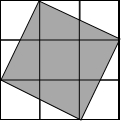如图，在3×3的方格中，有一阴影正方形，设每一个小方格的边长为1个单位．请解决下面的问题．