题目内容
14.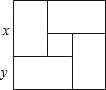 用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则矩形的长为7,宽为5.
用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则矩形的长为7,宽为5.
分析 设矩形的长为x,宽为y,表示出大正方形和小正方形的长和宽,然后根据大正方形的面积是144,小正方形的面积是4,列方程组求解.
解答 解:设矩形的长为x,宽为y,
由题意得,$\left\{\begin{array}{l}{(x+y)^{2}=144}\\{(x-y)^{2}=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=7}\\{y=5}\end{array}\right.$.
故答案为:7,5.
点评 本题考查了二元一次方程组的应用,解答本题的关键是读懂题意和图形,设出未知数,找出合适的等量关系,列方程组求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.有一块多边形草坪,在市政建设设计图纸上的面积为300cm2,其中一条边的长度为5cm,经测量,这条边的实际长度为15m,则这块草坪的实际面积是( )
| A. | 100m2 | B. | 270m2 | C. | 2 700m2 | D. | 90 000m2 |
3.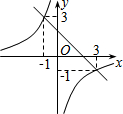 已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
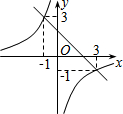 已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )| A. | x<-1或0<x<3 | B. | -1<x<0或x>3 | C. | -1<x<0 | D. | x>3 |
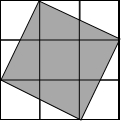 如图,在3×3的方格中,有一阴影正方形,设每一个小方格的边长为1个单位.请解决下面的问题.
如图,在3×3的方格中,有一阴影正方形,设每一个小方格的边长为1个单位.请解决下面的问题.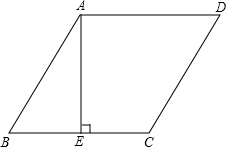 如图,在菱形ABCD中,AE⊥BC,垂足为E,EC=1,cosB=$\frac{5}{13}$.
如图,在菱形ABCD中,AE⊥BC,垂足为E,EC=1,cosB=$\frac{5}{13}$.