题目内容
12. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,若AB=8,则BD=2.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,若AB=8,则BD=2.
分析 已知Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,可求BC,在Rt△BCD中,利用互余关系求∠BCD=30°,再利用含30°的直角三角形的性质求BD.
解答 解:Rt△ABC中,
∵∠ACB=90°,∠A=30°,AB=8,
∴BC=$\frac{1}{2}$AB=4,
在Rt△BCD中,
∵∠B=90°-∠A=90°-30°=60°,
∴∠BCD=90°-∠B=30°,
∴BD=$\frac{1}{2}$BC=2.
故答案为:2.
点评 本题考查了含30°的直角三角形.含30°的直角三角形中,斜边等于30°角的对边的2倍,邻边等于30°角的对边的$\sqrt{3}$倍.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.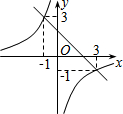 已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
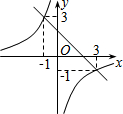 已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )
已知一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$在同一直角坐标系中的图象如图所示,则当y1>y2时,x的取值范围是( )| A. | x<-1或0<x<3 | B. | -1<x<0或x>3 | C. | -1<x<0 | D. | x>3 |
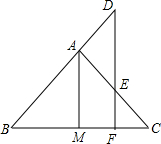 如图,在△ABC中,AB=AC,AM为△ABC底边上的中线,点D在BA的延长线上,E在AC上,且AD=AE,DE交BC于F,求证:DF⊥BC.
如图,在△ABC中,AB=AC,AM为△ABC底边上的中线,点D在BA的延长线上,E在AC上,且AD=AE,DE交BC于F,求证:DF⊥BC. 如图,是小明在镜中看到身后墙上的时钟,此时的实际时刻是11:20.
如图,是小明在镜中看到身后墙上的时钟,此时的实际时刻是11:20.