题目内容
13.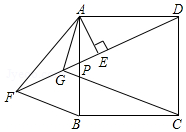 如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.(1)求证:△AEG是等腰直角三角形;
(2)求证:AG+CG=$\sqrt{2}$DG.
分析 (1)根据线段垂直平分线的定义得到AF=AD,根据等腰三角形的性质、角平分线的定义证明即可;
(2)作CH⊥DP,交DP于H点,证明△ADE≌△DCH(AAS),得到CH=DE,DH=AE=EG,证明CG=$\sqrt{2}$GH,AG=$\sqrt{2}$DH,计算即可.
解答 (1)证明:∵DE=EF,AE⊥DP,
∴AF=AD,
∴∠AFD=∠ADF,
∵∠ADF+∠DAE=∠PAE+∠DAE=90°,
∴∠AFD=∠PAE,
∵AG平分∠BAF,
∴∠FAG=∠GAP.
∵∠AFD+∠FAE=90°,
∴∠AFD+∠PAE+∠FAP=90°
∴2∠GAP+2∠PAE=90°,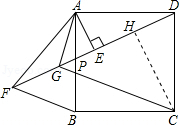
即∠GAE=45°,
∴△AGE为等腰直角三角形;
(2)证明:作CH⊥DP,交DP于H点,
∴∠DHC=90°.
∵AE⊥DP,
∴∠AED=90°,
∴∠AED=∠DHC.
∵∠ADE+∠CDH=90°,∠CDH+∠DCH=90°,
∴∠ADE=∠DCH.
∵在△ADE和△DCH中,
$\left\{\begin{array}{l}{∠AED=∠DHC}\\{∠ADE=∠DCH}\\{AD=DC}\end{array}\right.$,
∴△ADE≌△DCH(AAS),
∴CH=DE,DH=AE=EG.
∴EH+EG=EH+HD,
即GH=ED,
∴GH=CH.
∴CG=$\sqrt{2}$GH.
∵AG=$\sqrt{2}$EG,
∴AG=$\sqrt{2}$DH,
∴CG+AG=$\sqrt{2}$GH+$\sqrt{2}$HD,
∴CG+AG=$\sqrt{2}$(GH+HD),
即CG+AG=$\sqrt{2}$DG.
点评 本题考查的是正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质,掌握正方形的性质、全等三角形的判定定理和性质定理是解题的关键.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案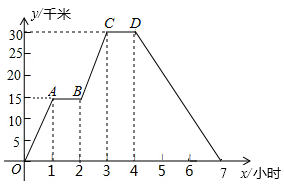 小明同学骑自行车沿平直路线行进,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
小明同学骑自行车沿平直路线行进,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.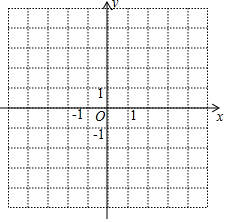 在如图所示的直角坐标系中,△ABC的顶点坐标分别为A(1,-4),B(5,-4),C(4,-1).
在如图所示的直角坐标系中,△ABC的顶点坐标分别为A(1,-4),B(5,-4),C(4,-1). 如图所示,△ABC在平面直角坐标系中,A,B,C的坐标分别是A(-3,3),B(-5,-1),C(-1,1); 点P(m,n)是△ABC内部的一点,平移△ABC,点A、B、C、P的对应点分别是A'、B'、C'、P'.且点P'的坐标为(m+4,n-2).
如图所示,△ABC在平面直角坐标系中,A,B,C的坐标分别是A(-3,3),B(-5,-1),C(-1,1); 点P(m,n)是△ABC内部的一点,平移△ABC,点A、B、C、P的对应点分别是A'、B'、C'、P'.且点P'的坐标为(m+4,n-2).

 B.
B.  C.
C.  D.
D. 