题目内容
1.不等式组$\left\{\begin{array}{l}{2x+1≥-1}\\{4+2x>3x}\end{array}\right.$的最小正整数解为1.分析 解不等式组,并求其整数解.
解答 解:$\left\{\begin{array}{l}{2x+1≥-1①}\\{4+2x>3x②}\end{array}\right.$,
由①得:2x>-2,
x>-1,
由②得:2x-3x>-4,
-x>-4,
x<4,
∴不等式组的解集为:-1<x<4,
∴不等式组的最小正整数解为:1;
故答案为:1.
点评 本题主要考查了一元一次不等式组的整数解,正确解出不等式组的解集是解决本题的关键;其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
相关题目
9.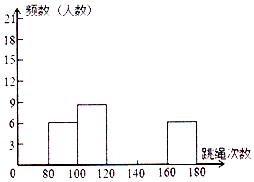 为了进一步了解七年级学生的身体素质情况,体育老师对七(1)班50为学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图.如图所示.请结合图表完成下列问题:
为了进一步了解七年级学生的身体素质情况,体育老师对七(1)班50为学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图.如图所示.请结合图表完成下列问题:
(1)表中的a=12;跳绳次数低于140次的有b人,b=26.
(2)请把频数分布直方图补充完整;
(3)若该校七年级学生一分钟跳绳次数为x,达标要求是:120≤x.请计算七(1)班的合格率.
 为了进一步了解七年级学生的身体素质情况,体育老师对七(1)班50为学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图.如图所示.请结合图表完成下列问题:
为了进一步了解七年级学生的身体素质情况,体育老师对七(1)班50为学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图.如图所示.请结合图表完成下列问题:| 组别 | 次数x | 频数 |
| 第1组 | 80≤x<100 | 6 |
| 第2组 | 100≤x<120 | 8 |
| 第3组 | 120≤x<140 | a |
| 第4组 | 140≤x<160 | 18 |
| 第5组 | 160≤x<180 | 6 |
(2)请把频数分布直方图补充完整;
(3)若该校七年级学生一分钟跳绳次数为x,达标要求是:120≤x.请计算七(1)班的合格率.
6.小明从A处出发沿正东方向行驶至B处,又沿东偏南15°方向行驶至C处,此时需把方向调整到向正东方向,则小明应该( )
| A. | 右转165° | B. | 左转165° | C. | 右转15° | D. | 左转15° |
2.若am=4,an=6,则am-n的值为( )
| A. | $\frac{2}{3}$ | B. | -2 | C. | 10 | D. | 24 |
 如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE.
如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE. 如图,已知A(n,-2),B(1,4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.
如图,已知A(n,-2),B(1,4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.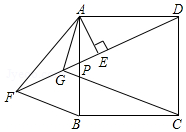 如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.