题目内容
18. 如图所示,△ABC在平面直角坐标系中,A,B,C的坐标分别是A(-3,3),B(-5,-1),C(-1,1); 点P(m,n)是△ABC内部的一点,平移△ABC,点A、B、C、P的对应点分别是A'、B'、C'、P'.且点P'的坐标为(m+4,n-2).
如图所示,△ABC在平面直角坐标系中,A,B,C的坐标分别是A(-3,3),B(-5,-1),C(-1,1); 点P(m,n)是△ABC内部的一点,平移△ABC,点A、B、C、P的对应点分别是A'、B'、C'、P'.且点P'的坐标为(m+4,n-2).(1)画出平移后的△A'B'C';
(2)求出四边形CBB'A'的面积;
(3)若△CBA'与△CP'A'的面积相等,则m+n的取值范围是-3<m+n<0.
分析 (1)根据网格结构找出点A′、B′、C′的位置,然后顺次连接即可;
(2)将四边形分割成两个三角形,然后利用三角形的面积公式列式计算即可得解;
(3)根据等底等高的三角形面积相等可得点P′与点B到CA′的距离相等,从而确定出点P′的位置,再根据点P′的坐标列出不等式和方程求出m的取值范围,n的值,然后求解即可.
解答 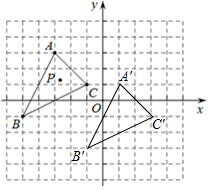 解:(1)△A'B'C'如图所示;
解:(1)△A'B'C'如图所示;
(2)四边形CBB'A'的面积=$\frac{1}{2}$×4×4+$\frac{1}{2}$×2×4,
=8+4,
=12;
(3)∵△CBA'与△CP'A'的面积相等,
∴点P′在经过点C′与x轴平行的△A′B′C′的内部线段上,
∴0<m+4<3,n-2=-1,
解得-4<m<-1,n=1,
∴-3<m+n<0.
故答案为:-3<m+n<0.
点评 本题考查了利用平移作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
9.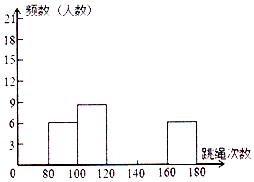 为了进一步了解七年级学生的身体素质情况,体育老师对七(1)班50为学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图.如图所示.请结合图表完成下列问题:
为了进一步了解七年级学生的身体素质情况,体育老师对七(1)班50为学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图.如图所示.请结合图表完成下列问题:
(1)表中的a=12;跳绳次数低于140次的有b人,b=26.
(2)请把频数分布直方图补充完整;
(3)若该校七年级学生一分钟跳绳次数为x,达标要求是:120≤x.请计算七(1)班的合格率.
 为了进一步了解七年级学生的身体素质情况,体育老师对七(1)班50为学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图.如图所示.请结合图表完成下列问题:
为了进一步了解七年级学生的身体素质情况,体育老师对七(1)班50为学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图.如图所示.请结合图表完成下列问题:| 组别 | 次数x | 频数 |
| 第1组 | 80≤x<100 | 6 |
| 第2组 | 100≤x<120 | 8 |
| 第3组 | 120≤x<140 | a |
| 第4组 | 140≤x<160 | 18 |
| 第5组 | 160≤x<180 | 6 |
(2)请把频数分布直方图补充完整;
(3)若该校七年级学生一分钟跳绳次数为x,达标要求是:120≤x.请计算七(1)班的合格率.
6.小明从A处出发沿正东方向行驶至B处,又沿东偏南15°方向行驶至C处,此时需把方向调整到向正东方向,则小明应该( )
| A. | 右转165° | B. | 左转165° | C. | 右转15° | D. | 左转15° |
19.若实数a、b、c满足$\sqrt{x+2}$+(y-3)2+|z+6|=0,则xyz的算术平方根是( )
| A. | 36 | B. | ±6 | C. | 6 | D. | $±\sqrt{6}$ |

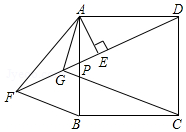 如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.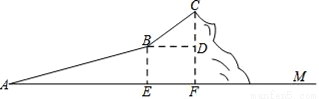
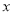 的一元二次方程
的一元二次方程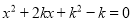 有两个不相等的实数根.
有两个不相等的实数根.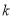 的取值范围;
的取值范围;