题目内容
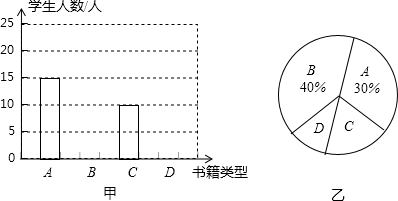
3．某校学生会向全校1900名学生发起了爱心捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图1和图2，请根据相关信息，解答系列问题：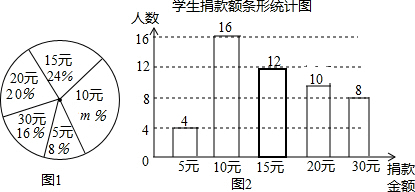
（1）本次接受随机抽样调查的学生人数为50人，图1中m的值是32．
（2）求本次调查获取的样本数据的平均数、众数和中位数；
（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．
分析 （1）根据统计图可以分别求得本次接受随机抽样调查的学生人数和图1中m的值；
（2）根据统计图可以分别得到本次调查获取的样本数据的平均数、众数和中位数；
（3）根据统计图中的数据可以估计该校本次活动捐款金额为10元的学生人数．
解答 解：（1）由统计图可得，
本次接受随机抽样调查的学生人数为：4÷8%=50，
m%=1-8%-16%-20%-24%=32%，
故答案为：50，32；
（2）本次调查获取的样本数据的平均数是：$\frac{4×5+16×10+12×15+10×20+8×30}{50}$=16（元），
本次调查获取的样本数据的众数是：10元，
本次调查获取的样本数据的中位数是：15元；
（3）该校本次活动捐款金额为10元的学生人数为：1900×$\frac{16}{50}$=608，
即该校本次活动捐款金额为10元的学生有608人．
点评 本题考查条形统计图、扇形统计图、用样本估计总体、中位数、众数，解题的关键是明确题意，找出所求问题需要的条件．
练习册系列答案
春雨教育同步作文系列答案
相关题目
13．
数学课上探究一次函数图象与反比例函数图象有交点时的相关结论：已知直线y=kx+b与x轴、y轴分别交于点C（x，0）、D（0，y），与双曲线y=$\frac{m}{x}$交于点A（x1，y1），B（x2，y2）．
（1）填空与观察：
（2）发现与验证：
数学学习小组在探究图象交点时发现以下结论：
①x1+x2=x；②y1+y2=y；③当b2+4mk≥0时，两函数图象一定会相交．
你认为以上探究的结论中正确的有①②③（填序号），请选择一个加以证明．
（3）应用与拓展：
连接AO，BO，判断△ACO与△BOD的面积有什么关系，并说明理由．
数学课上探究一次函数图象与反比例函数图象有交点时的相关结论：已知直线y=kx+b与x轴、y轴分别交于点C（x，0）、D（0，y），与双曲线y=$\frac{m}{x}$交于点A（x1，y1），B（x2，y2）．（1）填空与观察：
| 函数关系式 | C（x，0） | D（0，y） | A （x1，y1） | B（x2，y2） |
| y=2x+2，y=$\frac{4}{x}$，如图1 | （-1，0） | （0，2） | （1 ， 4） | （-2，-2） |
| y=x-3，y=$\frac{10}{x}$，如图2 | （3，0） | （0，-3） | （5，2） | （ -2， -5） |
数学学习小组在探究图象交点时发现以下结论：
①x1+x2=x；②y1+y2=y；③当b2+4mk≥0时，两函数图象一定会相交．
你认为以上探究的结论中正确的有①②③（填序号），请选择一个加以证明．
（3）应用与拓展：
连接AO，BO，判断△ACO与△BOD的面积有什么关系，并说明理由．
18．
如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第2017秒时，点P的坐标是（ ）
如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第2017秒时，点P的坐标是（ ）| A． | （2016，0） | B． | （2017，1） | C． | （2017，-1） | D． | （2018，0） |
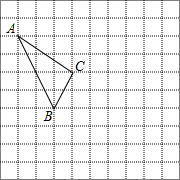在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为（-4，4），（-1，2）．
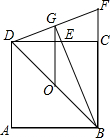如图，O是正方形ABCD的中心，BE平分∠DBC，交DC于点E，将点E绕着点C按顺时针方向旋转90°得到点F，连接CF，DF，BE的延长线交DF于点G，连接OG．