��Ŀ����
10����ͼ����ƽ��ֱ������ϵ�У�������y=a��x+2��2+4��x���ڵ�A��B����y���ڵ�D����C�������ߵĶ��㣬����AC��BC��OB=1����P��Q�ֱ����߶�AB��AC�ϵĶ��㣨��P����A��B���غϣ���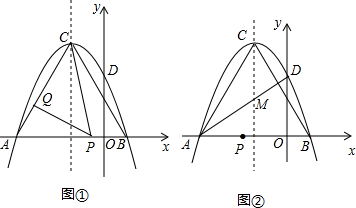
��1���������ߵĺ�����ϵʽ��
��2����ͼ�٣�����CPQ=��CAB���Ƿ���ڵ�Pʹ��CPQΪ���������Σ������P�����꣮
��3����ͼ�ڣ�����AD�������ߵĶԳ��ύ�ڵ�M�������������Ƿ����һ��N��ʹ�Ե�A��M��P��NΪ������ı���Ϊƽ���ı��Σ������ڣ�ֱ��д����N���ꣻ��������˵�����ɣ�
���� ��1����ΪOB=1������B������Ϊ��0��1�����ѽ�B��0��1�����������ߵĽ���ʽ�������a��ֵ��
��2����Pʹ��CPQΪ���������Σ��������������һ���ǡ�CPQ=��CQP����һ���ǡ�CPQ=��PCQ��
��3������A��M��P��NΪ������ı���Ϊƽ���ı��Σ�����N����������M����������ͬ���෴���������M�����꼴�ɣ������ֱ��AD�Ľ���ʽ��x=-2����ֱ��AD�Ľ���ʽ�������M�����꣮Ȼ��ע�����N�������Ҫ���۵�P��λ���Ƿ����߶�AB�ϣ�
��� �⣺��1����OB=1��
��B��������1��0����
��B��1��0������y=a��x+2��2+4��
��0=9a+4��
��a=-$\frac{4}{9}$��
�������ߵĽ���ʽΪy=-$\frac{4}{9}$��x+2��2+4��
��2������CPQ=��CQPʱ��
�ߡ�CPQ=��CAB��
���CQP=��CAB��
��ʱQ��A�غϣ�
��AC=PC��
���������ߵĶԳ��Կ�֪
��ʱP��B�غϣ����������⣬
����CPQ=��PCQʱ��
�ߡ�CPQ=��CAB��
���PCQ=��CAB��
��AP=PC��
��y=0����y=-$\frac{4}{9}$��x+2��2+4��
��x=-5��x=1��
��A��-5��0����
�߶���C������Ϊ��-2��4����
��AP2=��x+5��2��
PC2=��x+2��2+42��
�ࣨx+5��2=��x+2��2+42��
��x=-$\frac{5}{6}$��
��P��������-$\frac{5}{6}$��0����
��������������CPQ������������P��������-$\frac{5}{6}$��0����
��3�����P��������m��0����-5��m��1
��x=0����y=-$\frac{4}{9}$��x+2��2+4��
��y=$\frac{20}{9}$��
��D��������0��$\frac{20}{9}$����
��ֱ��AD�Ľ���ʽΪy=kx+b��
��A��-5��0����D��0��$\frac{20}{9}$������y=kx+b��
��$\left\{\begin{array}{l}{\frac{20}{9}=b}\\{0=-5k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{4}{9}}\\{b=\frac{20}{9}}\end{array}\right.$��
��ֱ��AD�Ľ���ʽΪy=$\frac{4}{9}$x+$\frac{20}{9}$��
��x=-2����y=$\frac{4}{9}$x+$\frac{20}{9}$��
��y=$\frac{4}{3}$��
��M��������-2��$\frac{4}{3}$����
����N��x���Ϸ�ʱ����ͼ1��
��ʱ��MN��AP��
��N��������Ϊ$\frac{4}{3}$��
��y=$\frac{4}{3}$����y=-$\frac{4}{9}$��x+2��2+4��
��x=-2��$\sqrt{6}$��
��N��������-2$��\sqrt{6}$��$\frac{4}{3}$����
��ʱ�Ե�A��M��P��NΪ������ı���Ϊƽ���ı���ʱ��
MN=AP=$\sqrt{6}$��
��m+5=$\sqrt{6}$
��m=-5+$\sqrt{6}$���������⣻
����N��x���·�ʱ��
����N��NF��x���ڵ�F��
�������ߵĶԳ�����x�ύ�ڵ�E��
��ʱN��������Ϊ-$\frac{4}{3}$��
��y=-$\frac{4}{3}$����y=-$\frac{4}{9}$��x+2��2+4��
��x=-2��2$\sqrt{3}$��
��x=-2-2$\sqrt{3}$ʱ����ͼ2��
�Ե�A��M��P��NΪ������ı���Ϊƽ���ı���ʱ��
��ʱAF=PE=2$\sqrt{3}$-3��
��-2-m=2$\sqrt{3}$-3��
��m=1-2$\sqrt{3}$���������⣬
��x=-2+2$\sqrt{3}$ʱ����ͼ3��
�Ե�A��M��P��NΪ������ı���Ϊƽ���ı���ʱ��
��ʱAE=PF=3��
��m-��-2+2$\sqrt{3}$��=3��
��m=1+2$\sqrt{3}$�����������⣬
�����������ڣ�
������������N������Ϊ��-2$��\sqrt{6}$��$\frac{4}{3}$����-2-2$\sqrt{3}$��-$\frac{4}{3}$��ʱ����A��M��P��NΪ������ı���Ϊƽ���ı��Σ�
���� ���⿼����κ������ۺ����⣬�漰����ϵ���������ʽ�����������ε��ж������ʣ�ƽ���ı��ε��ж���֪ʶ���ۺϳ̶Ƚϸߣ�����ѧ���������֪ʶ��������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | x1=x2=0 | B�� | x1=x2=2 | C�� | x1=0��x2=2 | D�� | x1=0��x2=-2 |