题目内容
15.已知x,y为实数,且y=$\sqrt{x-2014}$+$\sqrt{2014-x}$+1,则x+y+1=2016.分析 先根据二次根式的基本性质:$\sqrt{a}$有意义,则a≥0,依此求出x的值,进一步求得y的值,再代入计算即可求解.
解答 解:∵y=$\sqrt{x-2014}$+$\sqrt{2014-x}$+1,
∴x-2014≥0且2014-x≥0,
∴x=2014,
∴y=0+0+1=1,
∴x+y+1=2014+1+1=2016.
故答案为:2016.
点评 本题考查了二次根式有意义的条件,关键是熟悉知识点:二次根式的被开方数是非负数.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
6.已知a=20162,b=2015×2017,则( )
| A. | a=b | B. | a>b | C. | a<b | D. | a≤b |
20.下列图形中,不可以作为一个正方体的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
4.设681×2019-681×2018=a,2015×2016-2013×2018=b,$\sqrt{{{678}^2}+1358+690+678}=c$,则a,b,c的大小关系是( )
| A. | b<c<a | B. | a<c<b | C. | b<a<c | D. | c<b<a |
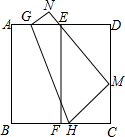 如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N
如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N